
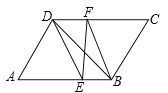
【题目】已知:如图所示,在![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的角平分线,交
的角平分线,交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() 、
、![]() 互相平分;
互相平分;
(2)若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)证明四边形DEBF是平行四边形即可;
(2)过D点作DG⊥AB于点G,通过已知可证△ADE是等边三角形,所以GE=2,DE=4,由勾股定理可求DG=![]() ,由
,由![]() ,得EB=2,所以GB=4,由勾股定理得
,得EB=2,所以GB=4,由勾股定理得![]() .
.
解:(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB-AE=CD-CF 即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形,
∴BD、EF互相平分;
(2)过D点作DG⊥AB于点G,
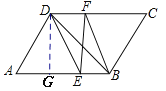
∵∠A=60°,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,![]()
∴![]()
∵AE=2EB,
∴BE=2,
∴GB=4,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】二次函数![]() (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
①16a﹣4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣![]() c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣![]() .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
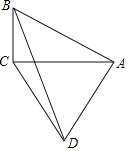
【题目】如图,AC,BD为四边形ABCD的对角线,AC⊥BC,AB⊥AD,CA=CD.若tan∠BAC=![]() .则tan∠DBC的值是( )
.则tan∠DBC的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户需求生产一种产品,成本每件20万元,规定每件售价不低于成本,且不高于40万元。经市场调查,每年的销售量y(件)与每件售价x(万元)满足一次函数关系,部分数据如下表:
售价x(万元/件) | 25 | 30 | 35 |
销售量y(件) | 50 | 40 | 30 |
(1)求y与x之间的函数表达式;
(2)设商品每年的总利润为W(万元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少万元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读):数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
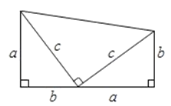
(理解):(1)如图,两个边长分别为![]() 、
、![]() 、
、![]() 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是![]() 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2,![]() 行
行![]() 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:
列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:![]() ________;
________;

(运用):(3)![]() 边形有
边形有![]() 个顶点,在它的内部再画
个顶点,在它的内部再画![]() 个点,以(
个点,以(![]() )个点为顶点,把
)个点为顶点,把![]() 边形剪成若干个三角形,设最多可以剪得
边形剪成若干个三角形,设最多可以剪得![]() 个这样的三角形.当
个这样的三角形.当![]() ,
,![]() 时,如图,最多可以剪得
时,如图,最多可以剪得![]() 个这样的三角形,所以
个这样的三角形,所以![]() .
.
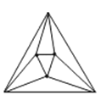
①当![]() ,
,![]() 时,如图,
时,如图,![]() ;当
;当![]() ,
,![]() 时,
时,![]() ;
;
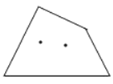
②对于一般的情形,在![]() 边形内画
边形内画![]() 个点,通过归纳猜想,可得
个点,通过归纳猜想,可得![]() (用含
(用含![]() 、
、![]() 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张相同的卡片,上面分别写有数字1、2、3、5,将卡片洗匀后背面朝上.
(1)从中任意抽取1张,抽得的卡片上数字为奇数的概率是_______;
(2)从中任意抽取1张,把上面的数字作为十位数,记录后不放回,再任意抽取1张把上面的数字作为个位数,求组成的两位数是3的倍数的概率.(用树状图或列表的方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
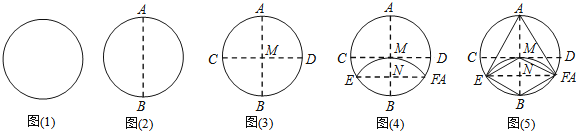
【题目】一张圆形纸片,小芳进行了如下连续操作:
![]() 将圆形纸片左右对折,折痕为AB,如图
将圆形纸片左右对折,折痕为AB,如图![]() .
.
![]() 将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图
将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图![]() .
.
![]() 将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图
将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图![]() .
.
![]() 连结AE、AF、BE、BF,如图
连结AE、AF、BE、BF,如图![]() .
.
经过以上操作,小芳得到了以下结论:
![]() ;
;![]() 四边形MEBF是菱形;
四边形MEBF是菱形;![]() 为等边三角形;
为等边三角形;![]() :
:![]() :
:![]() .以上结论正确的有
.以上结论正确的有![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长.
(2)求经过O,D,C三点的抛物线的解析式.
(3)一动点P从点C出发,沿CB以每秒2个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ.
(4)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,直接写出M点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
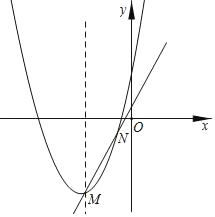
【题目】如图,已知抛物线y=x2+px+q的对称轴为直线x=﹣2,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(﹣1,﹣1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( ).
A. (0,﹣2) B. (0,﹣![]() ) C. (0,﹣
) C. (0,﹣![]() ) D. (0,﹣
) D. (0,﹣![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com