
【题目】(阅读):数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
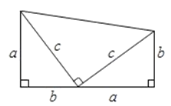
(理解):(1)如图,两个边长分别为![]() 、
、![]() 、
、![]() 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是![]() 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2,![]() 行
行![]() 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:
列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:![]() ________;
________;

(运用):(3)![]() 边形有
边形有![]() 个顶点,在它的内部再画
个顶点,在它的内部再画![]() 个点,以(
个点,以(![]() )个点为顶点,把
)个点为顶点,把![]() 边形剪成若干个三角形,设最多可以剪得
边形剪成若干个三角形,设最多可以剪得![]() 个这样的三角形.当
个这样的三角形.当![]() ,
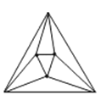
,![]() 时,如图,最多可以剪得
时,如图,最多可以剪得![]() 个这样的三角形,所以
个这样的三角形,所以![]() .
.
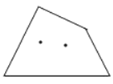
①当![]() ,
,![]() 时,如图,
时,如图,![]() ;当
;当![]() ,
,![]() 时,
时,![]() ;
;
②对于一般的情形,在![]() 边形内画
边形内画![]() 个点,通过归纳猜想,可得
个点,通过归纳猜想,可得![]() (用含
(用含![]() 、
、![]() 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
【答案】(1)见解析,故结论为:直角长分别为![]() 、
、![]() 斜边为
斜边为![]() 的直角三角形中
的直角三角形中![]() ;(2)
;(2)![]() ;(3)①6,3;②
;(3)①6,3;②![]() ,见解析.
,见解析.
【解析】
(1)此等腰梯形的面积有三部分组成,利用等腰梯形的面积等于三个直角三角形的面积之和列出方程并整理.
(2)由图可知![]() 行
行![]() 列的棋子排成一个正方形棋子个数为
列的棋子排成一个正方形棋子个数为![]() ,每层棋子分别为
,每层棋子分别为![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() .故可得用两种不同的方法计算棋子的个数,即可解答.
.故可得用两种不同的方法计算棋子的个数,即可解答.
(3)根据探画出图形究不难发现,三角形内部每增加一个点,分割部分增加![]() 部分,即可得出结论.
部分,即可得出结论.
(1)有三个![]() 其面积分别为
其面积分别为![]() ,
,![]() 和
和![]() .
.
直角梯形的面积为![]() .
.
由图形可知:![]()
![]()
整理得![]() ,
,![]() ,
,
![]()
![]() .
.
故结论为:直角长分别为![]() 、
、![]() 斜边为
斜边为![]() 的直角三角形中
的直角三角形中![]() .
.
(2)![]() 行
行![]() 列的棋子排成一个正方形棋子个数为
列的棋子排成一个正方形棋子个数为![]() ,每层棋子分别为
,每层棋子分别为![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() .
.
由图形可知:![]() .
.
故答案为:![]() .
.
(3)①如图,当![]() ,
,![]() 时,
时,![]() ,
,

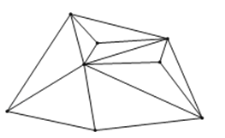
如图,当![]() ,
,![]() 时,
时,![]() .
.
②方法1.对于一般的情形,在![]() 边形内画
边形内画![]() 个点,第一个点将多边形分成了
个点,第一个点将多边形分成了![]() 个三角形,以后三角形
个三角形,以后三角形
内部每增加一个点,分割部分增加![]() 部分,故可得
部分,故可得![]() .
.
方法2.以![]() 的二个顶点和它内部的
的二个顶点和它内部的![]() 个点,共(
个点,共(![]() )个点为顶点,可把
)个点为顶点,可把![]() 分割成
分割成![]() 个互不重叠的小三角形.以四边形的
个互不重叠的小三角形.以四边形的![]() 个顶点和它内部的
个顶点和它内部的![]() 个点,共(
个点,共(![]() )个点为顶点,可把四边形分割成
)个点为顶点,可把四边形分割成![]() 个互不重叠的小三角形.故以
个互不重叠的小三角形.故以![]() 边形的
边形的![]() 个顶点和它内部的
个顶点和它内部的![]() 个点,共(
个点,共(![]() )个点作为顶点,可把原n边形分割成
)个点作为顶点,可把原n边形分割成![]() 个互不重叠的小三角形.故可得
个互不重叠的小三角形.故可得![]() .
.
故答案为:①![]() ,
,![]() ;②
;②![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,点P为∠MON的平分线上一点,以P点为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA·OB=OP2,我们就把∠APB叫作∠MON的智慧角.
(1)如图②,已知∠MON=90°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°,求证:∠APB是∠MON的智慧角;
(2)如图①,已知∠MON=α(0°<α<90°),OP=2,若∠APB是∠MON的智慧角,连接AB,用含α的式子分别表示∠APB的度数和△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
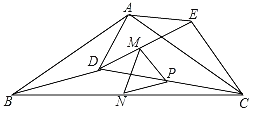
【题目】已知,△ABC和△ADE均为等腰三角形,AB=AC=5,AD=AE=2,且∠BAC=∠DAE=120°,把△ADE绕点A在平面内自由旋转.如图,连接BD,CD,CE,点M,P,N分别为DE,DC,BC的中点,连接MP,PN,MN,则△PMN的面积最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EFBF;②AG=2DC;③AE=EF;④AFEC=EFEB.其中正确的结论有( )
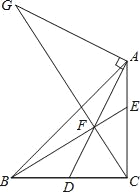
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
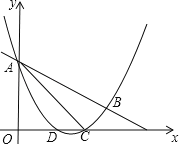
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下:
(1)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒![]() 个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
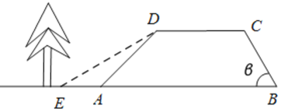
【题目】水坝的横截面是梯形ABCD,现测得坝顶DC=4 m,坡面AD的坡度i为1:1,坡面BC的坡角β为60°,坝高3m,(![]() )求:
)求:
(1)坝底AB的长(精确到0.1);
(2)水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度(如图),使新坡面DE的坡度i为![]() ,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2![]() x+m=0,有两个不相等的实数根.
x+m=0,有两个不相等的实数根.
⑴求实数m的最大整数值;
⑵在⑴的条下,方程的实数根是x1,x2,求代数式x12+x22-x1x2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
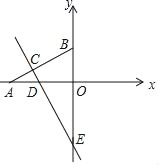
【题目】已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=![]() .
.
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y=![]() 的图象经过点C,求k的值;
的图象经过点C,求k的值;
(3)在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com