
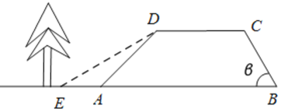
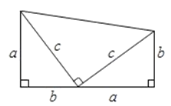
【题目】水坝的横截面是梯形ABCD,现测得坝顶DC=4 m,坡面AD的坡度i为1:1,坡面BC的坡角β为60°,坝高3m,(![]() )求:
)求:
(1)坝底AB的长(精确到0.1);
(2)水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度(如图),使新坡面DE的坡度i为![]() ,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
【答案】(1)AB≈8.73m;(2)没有影响;理由见解析.
【解析】
(1)根据坡度公式求出AH和BF的长,再加上FH的长度即可.(2)根据坡度公式求出EH的长度,进而求出AE长度,若小于2.5则没有影响.
如图,
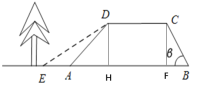
(1)分别过C,D作BE垂线,交BE于F,H,易得四边形CDHF是矩形,
∴CD=HF=4m,DH=CF=3m,
在Rt△ADH中,坡度i=1:1,
∴AH=DH=3m,
在Rt△BCF中,BC坡角为60 °,
∴BF=CF÷tan60°=√3≈1.73,
∴AB=AH+HF+FB=7+1.73=8.73m;
(2)Rt△EDH中,![]() =
=![]() ,∴EH=3√3,
,∴EH=3√3,
∴AE=EH-AH=3√3-3≈2.1m<2.5m,
所以没有影响.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
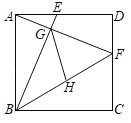
【题目】如图,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为( )
A.2![]() B.4
B.4![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
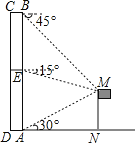
【题目】小甬工作的办公楼(矩形ABCD)前有一旗杆MN,MN⊥DN,旗杆高为12m,在办公楼底A处测得旗杆顶的仰角为30°,在办公楼天台B处测旗杆顶的仰角为45°,在小甬所在办公室楼层E处测得旗杆顶的俯角为15°.
(1)办公楼的高度AB;
(2)求小甬所在办公室楼层的高度AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读):数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
(理解):(1)如图,两个边长分别为![]() 、
、![]() 、
、![]() 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是![]() 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
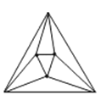
(2)如图2,![]() 行
行![]() 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:
列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:![]() ________;
________;

(运用):(3)![]() 边形有
边形有![]() 个顶点,在它的内部再画
个顶点,在它的内部再画![]() 个点,以(
个点,以(![]() )个点为顶点,把
)个点为顶点,把![]() 边形剪成若干个三角形,设最多可以剪得
边形剪成若干个三角形,设最多可以剪得![]() 个这样的三角形.当
个这样的三角形.当![]() ,
,![]() 时,如图,最多可以剪得
时,如图,最多可以剪得![]() 个这样的三角形,所以
个这样的三角形,所以![]() .
.
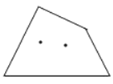
①当![]() ,
,![]() 时,如图,
时,如图,![]() ;当
;当![]() ,
,![]() 时,
时,![]() ;
;
②对于一般的情形,在![]() 边形内画
边形内画![]() 个点,通过归纳猜想,可得
个点,通过归纳猜想,可得![]() (用含
(用含![]() 、
、![]() 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
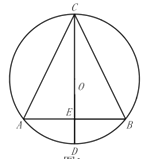
【题目】已知:![]() 内接于
内接于![]() ,直径
,直径![]() 交
交![]() 边于点
边于点![]() ,
,![]() .
.
(1)如图所示,求证:![]() ;
;
(2)如图所示,过点![]() 作
作![]() 于H,交
于H,交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图所示,在(2)的条件下,延长![]() 至点
至点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,射线
,射线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
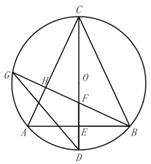
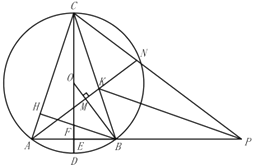
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张圆形纸片,小芳进行了如下连续操作:
![]() 将圆形纸片左右对折,折痕为AB,如图
将圆形纸片左右对折,折痕为AB,如图![]() .
.
![]() 将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图
将圆形纸片上下折叠,使A、B两点重合,折痕CD与AB相交于M,如图![]() .
.
![]() 将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图
将圆形纸片沿EF折叠,使B、M两点重合,折痕EF与AB相交于N,如图![]() .
.
![]() 连结AE、AF、BE、BF,如图
连结AE、AF、BE、BF,如图![]() .
.
经过以上操作,小芳得到了以下结论:
![]() ;
;![]() 四边形MEBF是菱形;
四边形MEBF是菱形;![]() 为等边三角形;
为等边三角形;![]() :
:![]() :
:![]() .以上结论正确的有
.以上结论正确的有![]()
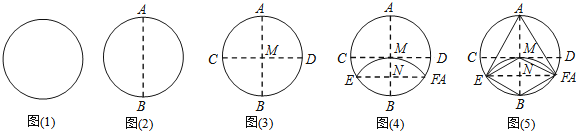
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的半径为
的半径为![]() 交
交![]() 于点D,点C是
于点D,点C是![]() 上一动点,以BC为边向下作等边
上一动点,以BC为边向下作等边![]() .
.
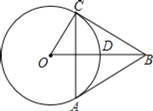
![]() 当点C运动到
当点C运动到![]() 时,
时,
![]() 求证:BC与
求证:BC与![]() 相切;
相切;
![]() 试判断点A是否在
试判断点A是否在![]() 上,并说明理由.
上,并说明理由.
![]() 设
设![]() 的面积为S,求S的取值范围.
的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
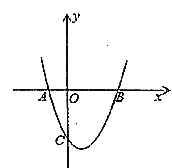
(1)求该抛物线的解析式;
(2)抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)设抛物线上有一个动点![]() ,当点
,当点![]() 在该抛物线上滑动到什么位置时,满足
在该抛物线上滑动到什么位置时,满足![]() ,并求出此时点
,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com