
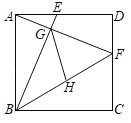
【题目】如图,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为( )
A.2![]() B.4
B.4![]() C.
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明调查了本校九年级300名学生到校的方式,根据调査结果绘制出统计图的一部分如图:
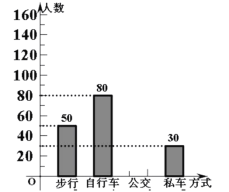
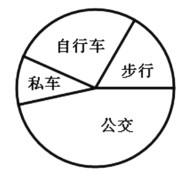
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)请估计在全校1200名学生中乘公交的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解本校学生的预防新型冠状病毒知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查,调查结果按了解程度分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调査结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:

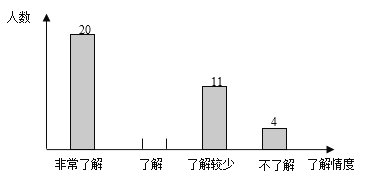
(1)本次调查的学生共有多少人?
(2)估计该校2000名学生中“了解”的人数约有多少人?
(3)若“不了解”的4人中有甲、乙两名男生,丙、丁两名女生,从这4人中随机抽取两人去重新参加预防新冠病毒如识培训,请用画树状图或列表的方法,求恰好抽到2名男生的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点P为∠MON的平分线上一点,以P点为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA·OB=OP2,我们就把∠APB叫作∠MON的智慧角.
(1)如图②,已知∠MON=90°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°,求证:∠APB是∠MON的智慧角;
(2)如图①,已知∠MON=α(0°<α<90°),OP=2,若∠APB是∠MON的智慧角,连接AB,用含α的式子分别表示∠APB的度数和△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.
(1)求证:CD是⊙O的切线;
(2)求证:CE=CF;
(3)若BD=1,CD=![]() ,求弦AC的长.
,求弦AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
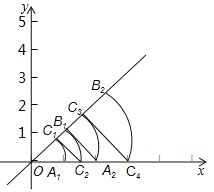
【题目】如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点C1,记![]() 长为m1;过点A1作A1B1垂直x轴,交直线l于点B1,以O为圆心,OB1为半径画弧,交x轴于C2,记
长为m1;过点A1作A1B1垂直x轴,交直线l于点B1,以O为圆心,OB1为半径画弧,交x轴于C2,记![]() 的长为m2;过点B1作A2B1垂直l,交x轴于点A2,以O为圆心,OA2为半径画弧,交直线l于C3,记
的长为m2;过点B1作A2B1垂直l,交x轴于点A2,以O为圆心,OA2为半径画弧,交直线l于C3,记![]() 的长为m3…按照这样规律进行下去,mn的长为( )
的长为m3…按照这样规律进行下去,mn的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
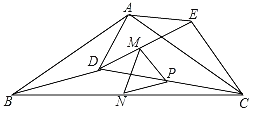
【题目】已知,△ABC和△ADE均为等腰三角形,AB=AC=5,AD=AE=2,且∠BAC=∠DAE=120°,把△ADE绕点A在平面内自由旋转.如图,连接BD,CD,CE,点M,P,N分别为DE,DC,BC的中点,连接MP,PN,MN,则△PMN的面积最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
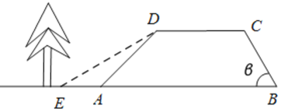
【题目】水坝的横截面是梯形ABCD,现测得坝顶DC=4 m,坡面AD的坡度i为1:1,坡面BC的坡角β为60°,坝高3m,(![]() )求:
)求:
(1)坝底AB的长(精确到0.1);
(2)水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度(如图),使新坡面DE的坡度i为![]() ,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com