
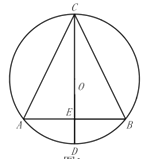
【题目】已知:![]() 内接于
内接于![]() ,直径
,直径![]() 交
交![]() 边于点
边于点![]() ,
,![]() .
.
(1)如图所示,求证:![]() ;
;
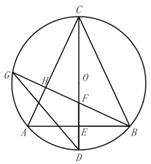
(2)如图所示,过点![]() 作
作![]() 于H,交
于H,交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
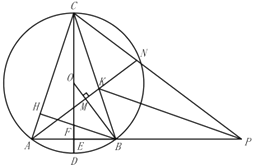
(3)如图所示,在(2)的条件下,延长![]() 至点
至点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,射线
,射线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)证明见解析;(2)证明见解析;(3)5
【解析】
(1)通过证明△AEC≌△BEC,得到![]() ;
;
(2)连接DB,AG,由(1)知CD⊥AB,∠ACD=∠BCD,再根据等角的余角相等和同弧所对的圆周角相等可得到∠GBA=∠BGD,∠GAB=∠BDG,进而证明△DBG≌△AGB(AAS),即可得到GD=AB;
(3)根据AM⊥OB,结合前两问结论,易证![]() ,
,![]() ,再根据AAA证明△ABK∽△CBA,△CAB∽△PAC,设半径为r,则AC=
,再根据AAA证明△ABK∽△CBA,△CAB∽△PAC,设半径为r,则AC=![]() AE=
AE=![]() ,由
,由![]() 得
得![]() ,可求得
,可求得![]() ,则
,则![]() ,再由PN=AN=
,再由PN=AN=![]() ,则
,则![]() ,由
,由![]() ,可求得
,可求得![]() .
.
解:(1)证明:∵CD为直径,![]() ,
,
∴CD⊥AB,
∴∠AEC=∠BEC=90°,
在△AEC和△BEC中,
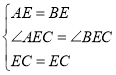 ,
,
∴△AEC≌△BEC,
∴![]() ;
;
(2)连接DB,AG,
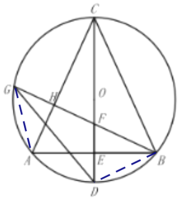
∵BG⊥AC,
∴∠HBA+∠HAB=90°,
由(1)知,CD⊥AB,∠ACD=∠BCD,
∴∠CAB+∠ACE=90°,
∴∠HBA=∠ACE,
∴∠GBA=∠BCD=∠BGD,
又∵∠GAB=∠BDG,
∴在△DBG和△AGB中,
 ,
,
∴△DBG≌△AGB(AAS),
∴GD=AB;
(3)连接BD,过点P作PQ⊥AN的延长线于N,
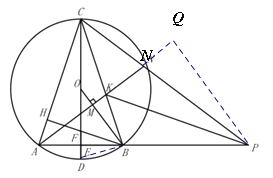
∵OD是![]() 的半径,AE=BE,
的半径,AE=BE,
∴OD⊥AB,
∵∠CFB为△CHF的外角,
∴∠CFB=∠CHF+∠HCF=90°+∠HCF,
∵∠CFB为△FEB的外角,
∴∠CFB=∠FEB+∠FBE=90°+∠FBE,
∴∠HCF=∠ABD,
∵∠HCF=∠ACD=∠ABD,
∴∠FBE=∠ABD,
∵∠BEF=∠BED,∠FBE=∠ABD,BE=BE,
∴△BFE≌△BDE,
∴FE=DE,
∵OF=AE,AE=BE,
∴OF=BE,
设FE=ED=a,OF=BE=b,
∴![]() ,
,
在Rt△OEB中,![]() ,
,
∴![]() ,
,
解得:![]() ,或
,或![]() (舍去),
(舍去),
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴∠KAB=∠EOB=2∠OCB=∠ACB,
而∠KBA=∠ABK,
∴△ABK∽△CBA,
∴∠KAB=∠ACB,
又∵AN=NP,
∴∠KAB=∠APN,
∴∠ACB=∠APN,
而∠CAB=∠PAC,
∴△CAB∽△PAC,
设半径为r,
则AC=![]() AE=
AE=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵PN=AN=![]() ,
,
则,![]() ,
,
∴![]() ,
,
得:![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆心为M的量角器的直径的两个端点A,B分别在x轴,y轴正半轴上(包括原点O),AB=4.点P,Q分别在量角器60°,120°刻度线外端,连结MP.量角器从点A与点Q重合滑动至点Q与点O重合的过程中,线段MP扫过的面积为( )
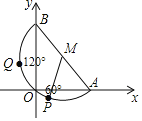
A.![]() π+
π+![]() B.
B.![]() πC.
πC.![]() π+2
π+2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
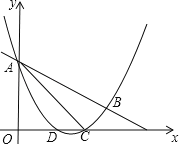
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下:
(1)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒![]() 个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
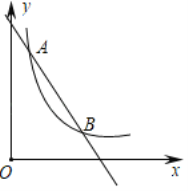
【题目】如图,一次函数![]() (k1、b为常数,k1≠0)的图象与反比例函数
(k1、b为常数,k1≠0)的图象与反比例函数![]()
![]() 的图象交于点A(m,8)与点B(4,2).
的图象交于点A(m,8)与点B(4,2).
①求一次函数与反比例函数的解析式.
②根据图象说明,当x为何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
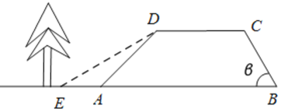
【题目】水坝的横截面是梯形ABCD,现测得坝顶DC=4 m,坡面AD的坡度i为1:1,坡面BC的坡角β为60°,坝高3m,(![]() )求:
)求:
(1)坝底AB的长(精确到0.1);
(2)水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度(如图),使新坡面DE的坡度i为![]() ,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
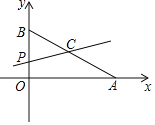
【题目】如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.﹣1≤t≤0B.﹣1≤t![]() C.
C.![]() D.t≤﹣1或t≥0
D.t≤﹣1或t≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
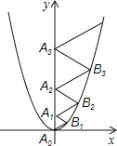
【题目】二次函数y=![]() x2的图象如图所示,点A0位于坐标原点,点A1、A
x2的图象如图所示,点A0位于坐标原点,点A1、A![]() 、A
、A![]() 、…、A
、…、A![]() 在y轴的正半轴上,点B
在y轴的正半轴上,点B![]() 、B
、B![]() 、B
、B![]() 、…、B
、…、B![]() 在二次函数y=
在二次函数y=![]() x2位于第一象限的图象上,若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形,则△A
x2位于第一象限的图象上,若△A0B1A1、△A1B2A2、△A2B3A3、…、△A2017B2018A2018都为等边三角形,则△A![]() B
B![]() A
A![]() 的边长=____________.
的边长=____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com