
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
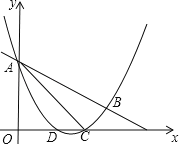
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下:
(1)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒![]() 个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
【答案】(Ⅰ)y=![]() x2﹣
x2﹣![]() x+3.tan∠BAC=
x+3.tan∠BAC=![]() ;(Ⅱ)(1)(11,36)、(
;(Ⅱ)(1)(11,36)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() );(2)点E的坐标为(2,1).
);(2)点E的坐标为(2,1).
【解析】
(Ⅰ)只需把A、C两点的坐标代入y=![]() x2+mx+n,就可得到抛物线的解析式,然后求出直线AB与抛物线的交点B的坐标,过点B作BH⊥x轴于H,如图1.易得∠BCH=∠ACO=45°,BC=
x2+mx+n,就可得到抛物线的解析式,然后求出直线AB与抛物线的交点B的坐标,过点B作BH⊥x轴于H,如图1.易得∠BCH=∠ACO=45°,BC=![]() ,AC=3
,AC=3![]() ,从而得到∠ACB=90°,然后根据三角函数的定义就可求出tan∠BAC的值;
,从而得到∠ACB=90°,然后根据三角函数的定义就可求出tan∠BAC的值;
(Ⅱ)(1)过点P作PG⊥y轴于G,则∠PGA=90°.设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x,易得∠APQ=∠ACB=90°.若点G在点A的下方,①当∠PAQ=∠CAB时,△PAQ∽△CAB.此时可证得△PGA∽△BCA,根据相似三角形的性质可得AG=3PG=3x.则有P(x,3-3x),然后把P(x,3-3x)代入抛物线的解析式,就可求出点P的坐标②当∠PAQ=∠CBA时,△PAQ∽△CBA,同理,可求出点P的坐标;若点G在点A的上方,同理,可求出点P的坐标;(2)过点E作EN⊥y轴于N,如图3.易得AE=![]() EN,则点M在整个运动中所用的时间可表示为
EN,则点M在整个运动中所用的时间可表示为![]() .作点D关于AC的对称点D′,连接D′E,则有D′E=DE,D′C=DC,∠D′CA=∠DCA=45°,从而可得∠D′CD=90°,DE+EN=D′E+EN.根据两点之间线段最短可得:当D′、E、N三点共线时,DE+EN=D′E+EN最小.此时可证到四边形OCD′N是矩形,从而有ND′=OC=3,ON=D′C=DC.然后求出点D的坐标,从而得到OD、ON、NE的值,即可得到点E的坐标.
.作点D关于AC的对称点D′,连接D′E,则有D′E=DE,D′C=DC,∠D′CA=∠DCA=45°,从而可得∠D′CD=90°,DE+EN=D′E+EN.根据两点之间线段最短可得:当D′、E、N三点共线时,DE+EN=D′E+EN最小.此时可证到四边形OCD′N是矩形,从而有ND′=OC=3,ON=D′C=DC.然后求出点D的坐标,从而得到OD、ON、NE的值,即可得到点E的坐标.
解:(Ⅰ)把A(0,3),C(3,0)代入y=![]() x2+mx+n,得
x2+mx+n,得
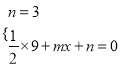 ,解得:
,解得: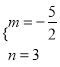 .
.
∴抛物线的解析式为y=![]() x2-
x2-![]() x+3.
x+3.
联立 ,解得:
,解得:![]() 或
或![]() ,
,
∴点B的坐标为(4,1).
过点B作BH⊥x轴于H,如图1.

∵C(3,0),B(4,1),
∴BH=1,OC=3,OH=4,CH=4-3=1,
∴BH=CH=1.
∵∠BHC=90°,
∴∠BCH=45°,BC=![]() .
.
同理:∠ACO=45°,AC=3![]() ,
,
∴∠ACB=180°-45°-45°=90°,
∴tan∠BAC=![]() ;
;
(Ⅱ)(1)存在点P,使得以A,P,Q为顶点的三角形与△ACB相似.
过点P作PG⊥y轴于G,则∠PGA=90°.
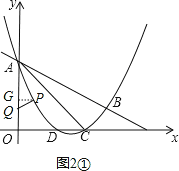
设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x.
∵PQ⊥PA,∠ACB=90°,
∴∠APQ=∠ACB=90°.
若点G在点A的下方,
①如图2①,当∠PAQ=∠CAB时,则△PAQ∽△CAB.
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,
∴△PGA∽△BCA,
∴![]() .
.
∴AG=3PG=3x.
则P(x,3-3x).
把P(x,3-3x)代入y=![]() x2-
x2-![]() x+3,得
x+3,得
![]() x2-
x2-![]() x+3=3-3x,
x+3=3-3x,
整理得:x2+x=0
解得:x1=0(舍去),x2=-1(舍去).
②如图2②,当∠PAQ=∠CBA时,则△PAQ∽△CBA.
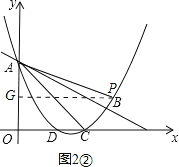
同理可得:AG=![]() PG=
PG=![]() x,则P(x,3-
x,则P(x,3-![]() x),
x),
把P(x,3-![]() x)代入y=
x)代入y=![]() x2-
x2-![]() x+3,得
x+3,得
![]() x2-
x2-![]() x+3=3-
x+3=3-![]() x,
x,
整理得:x2-![]() x=0
x=0
解得:x1=0(舍去),x2=![]() ,
,
∴P(![]() ,
,![]() );
);
若点G在点A的上方,
①当∠PAQ=∠CAB时,则△PAQ∽△CAB,
同理可得:点P的坐标为(11,36).
②当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:点P的坐标为P(![]() ,
,![]() ).
).
综上所述:满足条件的点P的坐标为(11,36)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() );
);
(2)过点E作EN⊥y轴于N,如图3.
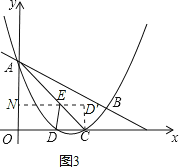
在Rt△ANE中,EN=AEsin45°=![]() AE,即AE=
AE,即AE=![]() EN,
EN,
∴点M在整个运动中所用的时间为![]() .
.
作点D关于AC的对称点D′,连接D′E,
则有D′E=DE,D′C=DC,∠D′CA=∠DCA=45°,
∴∠D′CD=90°,DE+EN=D′E+EN.
根据两点之间线段最短可得:
当D′、E、N三点共线时,DE+EN=D′E+EN最小.
此时,∵∠D′CD=∠D′NO=∠NOC=90°,
∴ND′=OC=3,ON=D′C=DC.
对于y=![]() x2-
x2-![]() x+3,
x+3,
当y=0时,有![]() x2-
x2-![]() x+3=0,
x+3=0,
解得:x1=2,x2=3.
∴D(2,0),OD=2,
∴ON=DC=OC-OD=3-2=1,
∴NE=AN=AO-ON=3-1=2,
∴点E的坐标为(2,1).


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
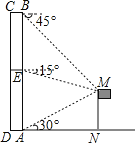
【题目】小甬工作的办公楼(矩形ABCD)前有一旗杆MN,MN⊥DN,旗杆高为12m,在办公楼底A处测得旗杆顶的仰角为30°,在办公楼天台B处测旗杆顶的仰角为45°,在小甬所在办公室楼层E处测得旗杆顶的俯角为15°.
(1)办公楼的高度AB;
(2)求小甬所在办公室楼层的高度AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接暑假旅游高峰的到来,某旅游纪念品商店决定购进A、B两种纪念品.若购进A种纪念品7件,B种纪念品4件,需要760元;若购进A种纪念品5件.B种纪念品8件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件.考虑市场需求和资金周转,这100件纪念品的资金不少于7000元,但不超过7200元,那么该商店共有几种进货方案?
(3)若销售A种纪念品每件可获利润30元,B种纪念品每件可获利润20元,用(2)中的进货方案,哪一种方案可获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读):数学中,常对同一个量(图形的面积、点的个数、三角形的内角和等)用两种不同的方法计算,从而建立相等关系,我们把这一思想称为“算两次”.“算两次”也称做富比尼原理,是一种重要的数学思想.
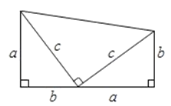
(理解):(1)如图,两个边长分别为![]() 、
、![]() 、
、![]() 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是![]() 的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
(2)如图2,![]() 行
行![]() 列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:
列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:![]() ________;
________;

(运用):(3)![]() 边形有
边形有![]() 个顶点,在它的内部再画
个顶点,在它的内部再画![]() 个点,以(
个点,以(![]() )个点为顶点,把
)个点为顶点,把![]() 边形剪成若干个三角形,设最多可以剪得
边形剪成若干个三角形,设最多可以剪得![]() 个这样的三角形.当
个这样的三角形.当![]() ,
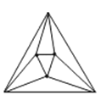
,![]() 时,如图,最多可以剪得
时,如图,最多可以剪得![]() 个这样的三角形,所以
个这样的三角形,所以![]() .
.
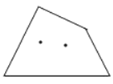
①当![]() ,
,![]() 时,如图,
时,如图,![]() ;当
;当![]() ,
,![]() 时,
时,![]() ;
;
②对于一般的情形,在![]() 边形内画
边形内画![]() 个点,通过归纳猜想,可得
个点,通过归纳猜想,可得![]() (用含
(用含![]() 、
、![]() 的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
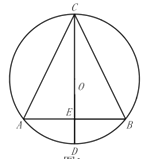
【题目】已知:![]() 内接于
内接于![]() ,直径
,直径![]() 交
交![]() 边于点
边于点![]() ,
,![]() .
.
(1)如图所示,求证:![]() ;
;
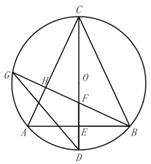
(2)如图所示,过点![]() 作
作![]() 于H,交
于H,交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
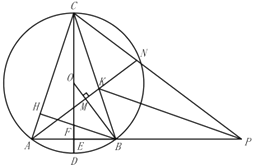
(3)如图所示,在(2)的条件下,延长![]() 至点
至点![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,射线
,射线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
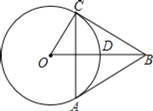
【题目】如图,![]() 的半径为
的半径为![]() 交
交![]() 于点D,点C是
于点D,点C是![]() 上一动点,以BC为边向下作等边
上一动点,以BC为边向下作等边![]() .
.
![]() 当点C运动到
当点C运动到![]() 时,
时,
![]() 求证:BC与
求证:BC与![]() 相切;
相切;
![]() 试判断点A是否在
试判断点A是否在![]() 上,并说明理由.
上,并说明理由.
![]() 设
设![]() 的面积为S,求S的取值范围.
的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com