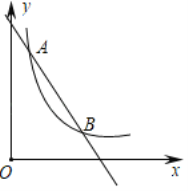
【题目】如图，一次函数
（k1、b为常数，k1≠0）的图象与反比例函数
的图象交于点A（m，8）与点B（4，2）．
①求一次函数与反比例函数的解析式．
②根据图象说明，当x为何值时，
．
科目：初中数学 来源： 题型：
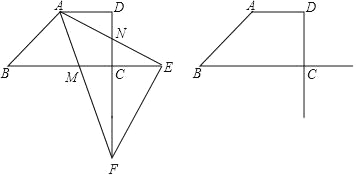
【题目】如图，梯形ABCD中，AD∥BC，DC⊥BC，且∠B=45°，AD=DC=1，点M为边BC上一动点，联结AM并延长交射线DC于点F，作∠FAE=45°交射线BC于点E、交边DCN于点N，联结EF．
（1）当CM：CB=1：4时，求CF的长．
（2）设CM=x，CE=y，求y关于x的函数关系式，并写出定义域．
（3）当△ABM∽△EFN时，求CM的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
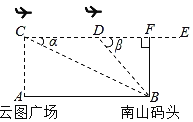
【题目】兴隆湖是成都天府新区著名的生态绿地工程．在一次户外综合实践活动中，小明同学所在的兴趣小组用无人机航拍测量云图广场A与南山码头B的直线距离．由于无人机控制距离有限，为了安全，不能直接测量，他们采用如下方法：如图，小明在云图广场A的正上方点C处测得南山码头B的俯角α＝17.09°；接着无人机往南山码头B方向水平飞行0.9千米到达点D处，测得此时南山码头B的俯角β＝45°．已知AC⊥AB，CD∥AB，请根据测量数据计算A，B两地的距离．（结果精确到0.1km，参考数据：sinα≈0.29，tanα≈0.31，sinβ≈0.71）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为迎接暑假旅游高峰的到来，某旅游纪念品商店决定购进A、B两种纪念品．若购进A种纪念品7件，B种纪念品4件，需要760元；若购进A种纪念品5件．B种纪念品8件，需要800元．
（1）求购进A、B两种纪念品每件各需多少元？
（2）若该商店决定购进这两种纪念品共100件．考虑市场需求和资金周转，这100件纪念品的资金不少于7000元，但不超过7200元，那么该商店共有几种进货方案？
（3）若销售A种纪念品每件可获利润30元，B种纪念品每件可获利润20元，用（2）中的进货方案，哪一种方案可获利最大？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2016年，某贫困户的家庭年人均纯收入为2500元，通过政府产业扶持，发展了养殖业后，到2018年，家庭年人均纯收入达到了3600元．
（1）求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率；
（2）若年平均增长率保持不变，2019年该贫困户的家庭年人均纯收入是否能达到4200元？
查看答案和解析>>
科目：初中数学 来源： 题型：
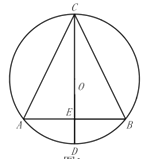
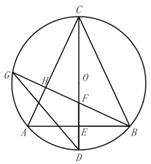
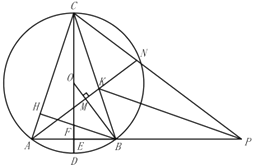
【题目】已知：
内接于
，直径
交
边于点
，
．
（1）如图所示，求证：
；
（2）如图所示，过点
作
于H，交于
，交于点
，连接
，求证：
；
（3）如图所示，在（2）的条件下，延长至点
，连接
、
，过点
作
于
，射线
交
于点
，交于点
，连接
，
，若
，
，求的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
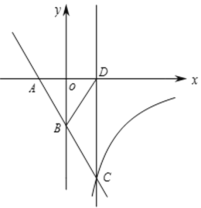
【题目】已知直线：y1＝
与x轴、y轴相交于A、B两点，与双曲线
(k＜0，x＞0)相交于第四象限的点C，过点C作直线l⊥x轴，垂足为D，若△ABD的面积为
，且B是AC的中点．
(1)求k的值；
(2)直接写出
的解集；
(3)若P为直线l的一动点，点P的纵坐标为m，∠APB≥30°，求m的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（12分）某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出5件．
（1）若商场平均每天要盈利1600元，每件衬衫应降价多少元？
（2）若该商场要每天盈利最大，每件衬衫应降价多少元？盈利最大是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
图象的一部分如图所示，给出以下结论：
；
当
时，函数有最大值；
方程
的解是
，
；
，其中结论错误的个数是
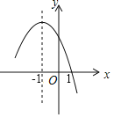
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
