
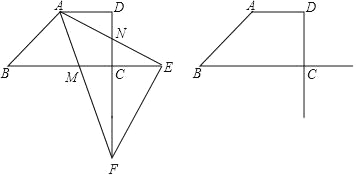
【题目】如图,梯形ABCD中,AD∥BC,DC⊥BC,且∠B=45°,AD=DC=1,点M为边BC上一动点,联结AM并延长交射线DC于点F,作∠FAE=45°交射线BC于点E、交边DCN于点N,联结EF.
(1)当CM:CB=1:4时,求CF的长.
(2)设CM=x,CE=y,求y关于x的函数关系式,并写出定义域.
(3)当△ABM∽△EFN时,求CM的长.
【答案】(1) CF=1;(2)y=![]() ,0≤x≤1;(3)CM=2﹣
,0≤x≤1;(3)CM=2﹣![]() .
.
【解析】
(1)如图1中,作AH⊥BC于H.首先证明四边形AHCD是正方形,求出BC、MC的长,利用平行线分线段成比例定理即可解决问题;
(2)在Rt△AEH中,AE2=AH2+EH2=12+(1+y)2,由△EAM∽△EBA,可得![]() ,推出AE2=EMEB,由此构建函数关系式即可解决问题;
,推出AE2=EMEB,由此构建函数关系式即可解决问题;
(3)如图2中,作AH⊥BC于H,连接MN,在HB上取一点G,使得HG=DN,连接AG.想办法证明CM=CN,MN=DN+HM即可解决问题;
解:(1)如图1中,作AH⊥BC于H.
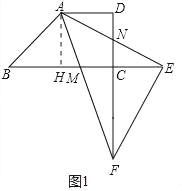
∵CD⊥BC,AD∥BC,
∴∠BCD=∠D=∠AHC=90°,
∴四边形AHCD是矩形,
∵AD=DC=1,
∴四边形AHCD是正方形,
∴AH=CH=CD=1,
∵∠B=45°,
∴AH=BH=1,BC=2,
∵CM=![]() BC=
BC=![]() ,CM∥AD,
,CM∥AD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴CF=1.
(2)如图1中,在Rt△AEH中,AE2=AH2+EH2=12+(1+y)2,
∵∠AEM=∠AEB,∠EAM=∠B,
∴△EAM∽△EBA,
∴![]() =
=![]() ,
,
∴AE2=EMEB,
∴1+(1+y)2=(x+y)(y+2),
∴y=![]() ,
,
∵2﹣2x≥0,
∴0≤x≤1.
(3)如图2中,作AH⊥BC于H,连接MN,在HB上取一点G,使得HG=DN,连接AG.
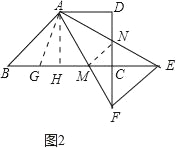
则△ADN≌△AHG,△MAN≌△MAG,
∴MN=MG=HM+GH=HM+DN,
∵△ABM∽△EFN,
∴∠EFN=∠B=45°,
∴CF=CE,
∵四边形AHCD是正方形,
∴CH=CD=AH=AD,EH=DF,∠AHE=∠D=90°,
∴△AHE≌△ADF,
∴∠AEH=∠AFD,
∵∠AEH=∠DAN,∠AFD=∠HAM,
∴∠HAM=∠DAN,
∴△ADN≌△AHM,
∴DN=HM,设DN=HM=x,则MN=2x,CN=CM=![]() x,
x,
∴x+![]() x=1,
x=1,
![]() ﹣1,
﹣1,
∴CM=2﹣![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD的值最小时,点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD的值最小时,点P的坐标为( )

A.(﹣1,0)B.(﹣2,0)C.(﹣3,0)D.(﹣4,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
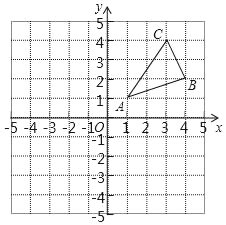
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆高铁与一辆动车组列车在长为1320千米的京沪高速铁路上运行,已知高铁列车比动车组列车平均速度每小时快99千米,且高铁列车比动车组列车全程运行时间少3小时,求这辆高铁列车全程运行的时间和平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 分别是射线
分别是射线![]() 、
、![]() 上的动点,且点
上的动点,且点![]() 不与点
不与点![]() 、
、![]() 重合,
重合,![]() .
.

(1)如图1,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的周长;
的周长;
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,设
的延长线上时,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,请猜想
,请猜想![]() 与
与![]() 之间的等量关系,并证明你的猜想.
之间的等量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com