
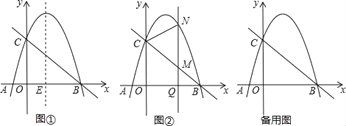
ΓΨΧβΡΩΓΩ»γΆΦΔΌ“―÷Σ≈ΉΈοœΏy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©ΒΡΆΦœσ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®A‘ΎBΒΡΉσ≤ύΘ©Θ§”κyΒΡ’ΐΑκ÷αΫΜ”ΎΒψCΘ§Ν§ΫαBCΘ§Εΰ¥ΈΚ· ΐΒΡΕ‘≥Τ÷α”κx÷αΒΡΫΜΒψΈΣEΘ°
Θ®1Θ©≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κx÷αΒΡΫΜΒψEΉχ±ξΈΣ_____Θ§ΒψAΒΡΉχ±ξΈΣ_____ΘΜ
Θ®2Θ©»τ“‘EΈΣ‘≤–ΡΒΡ‘≤”κy÷αΚΆ÷±œΏBCΕΦœύ«–Θ§ ‘«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§»γΆΦΔΎQΘ®mΘ§0Θ© «xΒΡ’ΐΑκ÷α…œ“ΜΒψΘ§ΙΐΒψQΉςy÷αΒΡΤΫ––œΏΘ§”κ÷±œΏBCΫΜ”ΎΒψMΘ§”κ≈ΉΈοœΏΫΜ”ΎΒψNΘ§Ν§ΫαCNΘ§ΫΪΓςCMN―ΊCNΖ≠’έΘ§MΒΡΕ‘”ΠΒψΈΣMΓδΘ°‘ΎΆΦΔΎ÷–ΧΫΨΩΘΚ «Ζώ¥φ‘ΎΒψQΘ§ ΙΒΟMΓδ«ΓΚΟ¬δ‘Ύy÷α…œΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωQΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©(1.5Θ§0) (-1Θ§0)
Θ®2Θ©![]() ΘΜ
ΘΜ
Θ®3Θ©¥φ‘ΎΘ§![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©”…≈ΉΈοœΏ![]() ΒΡΕ‘≥Τ÷αΈΣ÷±œΏ
ΒΡΕ‘≥Τ÷αΈΣ÷±œΏ![]() «σ≥ω≈ΉΈοœΏy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©ΒΡΕ‘≥Τ÷αΖΫ≥ΧΘ§Φ¥Ω…«σΒΟΒψEΒΡΉχ±ξΘΜ‘Ύy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©Ννy=0Ω…ΒΟΙΊ”ΎxΒΡΖΫ≥Χax2©¹3ax©¹4a=0Θ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟΒψAΒΡΉχ±ξΘΜ
«σ≥ω≈ΉΈοœΏy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©ΒΡΕ‘≥Τ÷αΖΫ≥ΧΘ§Φ¥Ω…«σΒΟΒψEΒΡΉχ±ξΘΜ‘Ύy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©Ννy=0Ω…ΒΟΙΊ”ΎxΒΡΖΫ≥Χax2©¹3ax©¹4a=0Θ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟΒψAΒΡΉχ±ξΘΜ
Θ®2Θ©»γΆΦ1Θ§…ηΓ―E”κ÷±œΏBCœύ«–”ΎΒψDΘ§Ν§Ϋ”DEΘ§‘ρDEΓΆBCΘ§ΫαΚœΘ®1Θ©Ω…ΒΟDE=OE=![]() Θ§EB=
Θ§EB=![]() Θ§OC=-4aΘ§‘ΎRtΓςBDE÷–”…Ι¥Ι…Ε®άμΩ…ΒΟBD=2Θ§’β―υ”…tanΓœOBC=
Θ§OC=-4aΘ§‘ΎRtΓςBDE÷–”…Ι¥Ι…Ε®άμΩ…ΒΟBD=2Θ§’β―υ”…tanΓœOBC=![]() Φ¥Ω…Ν–≥ωΙΊ”ΎaΒΡΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σΒΟaΒΡ÷ΒΦ¥Ω…ΒΟΒΫ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Φ¥Ω…Ν–≥ωΙΊ”ΎaΒΡΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σΒΟaΒΡ÷ΒΦ¥Ω…ΒΟΒΫ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©”…’έΒΰΒΡ–‘÷ ΚΆMNΓΈy÷αΩ…ΒΟΓœMCN=ΓœMΓδCN=ΓœMNCΘ§”…¥ΥΩ…ΒΟCM=MNΘ§”…ΒψBΒΡΉχ±ξΈΣΘ®4Θ§0Θ©Θ§ΒψCΒΡΉχ±ξΈΣΘ®0Θ§3Θ©Ω…ΒΟœΏΕΈBC=5Θ§÷±œΏBCΒΡΫβΈω ΫΈΣy=©¹![]() x+3Θ§”…¥ΥΦ¥Ω…ΒΟΒΫMΓΔNΒΡΉχ±ξΖ÷±πΈΣΘ®mΘ§©¹
x+3Θ§”…¥ΥΦ¥Ω…ΒΟΒΫMΓΔNΒΡΉχ±ξΖ÷±πΈΣΘ®mΘ§©¹![]() m+3Θ©ΓΔΘ®mΘ§©¹
m+3Θ©ΓΔΘ®mΘ§©¹![]() m2+
m2+![]() m+3Θ©Θ§ΉςMFΓΆOC”ΎFΘ§’β―υ”…sinΓœBCO=
m+3Θ©Θ§ΉςMFΓΆOC”ΎFΘ§’β―υ”…sinΓœBCO=![]() Φ¥Ω…ΫβΒΟCM=
Φ¥Ω…ΫβΒΟCM=![]() mΘ§»ΜΚσΖ÷ΒψN‘Ύ÷±œΏBCΒΡ…œΖΫΚΆœ¬ΖΫΝΫ÷÷«ιΩω”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ¥ο≥ωMNΒΡ≥ΛΕ»Θ§ΫαΚœMN=CMΦ¥Ω…Ν–≥ωΙΊ”ΎmΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟΕ‘”ΠΒΡmΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΕ‘”ΠΒΡΒψQΒΡΉχ±ξ.
mΘ§»ΜΚσΖ÷ΒψN‘Ύ÷±œΏBCΒΡ…œΖΫΚΆœ¬ΖΫΝΫ÷÷«ιΩω”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ¥ο≥ωMNΒΡ≥ΛΕ»Θ§ΫαΚœMN=CMΦ¥Ω…Ν–≥ωΙΊ”ΎmΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟΕ‘”ΠΒΡmΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΕ‘”ΠΒΡΒψQΒΡΉχ±ξ.
Θ®1Θ©ΓΏΕ‘≥Τ÷αx=![]() Θ§
Θ§
ΓύΒψEΉχ±ξΘ®![]() Θ§0Θ©Θ§
Θ§0Θ©Θ§
Ννy=0Θ§‘ρ”–ax2©¹3ax©¹4a=0Θ§
Γύx=©¹1Μρ4Θ§
ΓύΒψAΉχ±ξΘ®©¹1Θ§0Θ©Θ°
Ι ¥πΑΗΖ÷±πΈΣΘ®![]() Θ§0Θ©Θ§Θ®©¹1Θ§0Θ©Θ°
Θ§0Θ©Θ§Θ®©¹1Θ§0Θ©Θ°
Θ®2Θ©»γΆΦΔΌ÷–Θ§…ηΓ―E”κ÷±œΏBCœύ«–”ΎΒψDΘ§Ν§Ϋ”DEΘ§‘ρDEΓΆBCΘ§
ΓΏDE=OE=![]() Θ§EB=
Θ§EB=![]() Θ§OC=©¹4aΘ§
Θ§OC=©¹4aΘ§
ΓύDB=![]() Θ§
Θ§
ΓΏtanΓœOBC=![]() Θ§
Θ§
Γύ![]() Θ§ΫβΒΟa=
Θ§ΫβΒΟa=![]() Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣy=![]() Θ°
Θ°
Θ®3Θ©»γΆΦΔΎ÷–Θ§”…Χβ“βΓœMΓδCN=ΓœNCBΘ§
ΓΏMNΓΈOMΓδΘ§
ΓύΓœMΓδCN=ΓœCNMΘ§
ΓύMN=CMΘ§
ΓΏΒψBΒΡΉχ±ξΈΣΘ®4Θ§0Θ©Θ§ΒψCΒΡΉχ±ξΈΣΘ®0Θ§3Θ©Θ§
Γύ ÷±œΏBCΫβΈω ΫΈΣy=©¹![]() x+3Θ§BC=5Θ§
x+3Θ§BC=5Θ§
ΓύMΘ®mΘ§©¹![]() m+3Θ©Θ§NΘ®mΘ§©¹
m+3Θ©Θ§NΘ®mΘ§©¹![]() m2+
m2+![]() m+3Θ©Θ§ΉςMFΓΆOC”ΎFΘ§
m+3Θ©Θ§ΉςMFΓΆOC”ΎFΘ§
ΓΏsinΓœBCO=![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύCM=![]() mΘ§
mȧ
ΔΌΒ±N‘Ύ÷±œΏBC…œΖΫ ±Θ§©¹![]() x2+
x2+![]() x+3©¹Θ®©¹
x+3©¹Θ®©¹![]() x+3Θ©=
x+3ȩ=![]() mȧ
mȧ
ΫβΒΟΘΚm=![]() Μρ0Θ®…αΤζΘ©Θ§
Μρ0Θ®…αΤζΘ©Θ§
ΓύQ1Θ®![]() Θ§0Θ©Θ°
Θ§0Θ©Θ°
ΔΎΒ±N‘Ύ÷±œΏBCœ¬ΖΫ ±Θ§Θ®©¹![]() m+3Θ©©¹Θ®©¹
m+3Θ©©¹Θ®©¹![]() m2+
m2+![]() m+3Θ©=
m+3ȩ=![]() mȧ
mȧ
ΫβΒΟm=![]() Μρ0Θ®…αΤζΘ©Θ§
Μρ0Θ®…αΤζΘ©Θ§
ΓύQ2Θ®![]() Θ§0Θ©Θ§
Θ§0Θ©Θ§
Ήέ…œΥυ ωΘΚΒψQΉχ±ξΈΣΘ®![]() Θ§0Θ©ΜρΘ®
Θ§0Θ©ΜρΘ®![]() Θ§0Θ©Θ°
Θ§0Θ©Θ°




 –¬Χβ–Ά»Ϊ≥ΧΦλ≤βΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ
–¬Χβ–Ά»Ϊ≥ΧΦλ≤βΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
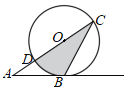
ΓΨΧβΡΩΓΩ»γΆΦΘ§Γ―OΒΡ‘≤–ΡO‘ΎΓςABCΒΡ±ΏAC…œΘ§AC”κΓ―OΖ÷±πΫΜ”ΎCΘ§DΝΫΒψΘ§Γ―O”κ±ΏABœύ«–Θ§«“«–Βψ«ΓΈΣΒψBΘ°
Θ®1Θ©«σ÷ΛΘΚΓœA+2ΓœCΘΫ90ΓψΘΜ
Θ®2Θ©»τΓœAΘΫ30ΓψΘ§ABΘΫ6Θ§«σΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΘΚΙΊ”ΎxΒΡΕΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσ”κx÷αΫΜ”ΎΒψA(1Θ§0)ΚΆΒψBΘ§”κy÷αΫΜ”ΎΒψC(0Θ§3)Θ§≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κx÷αΫΜ”ΎΒψD.
ΒΡΆΦœσ”κx÷αΫΜ”ΎΒψA(1Θ§0)ΚΆΒψBΘ§”κy÷αΫΜ”ΎΒψC(0Θ§3)Θ§≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κx÷αΫΜ”ΎΒψD.
(1)«σΕΰ¥ΈΚ· ΐΒΡ±μ¥ο ΫΘΜ
(2)‘Ύy÷α…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§ ΙΓςPBCΈΣΒ»―ϋ»ΐΫ«–Έ.»τ¥φ‘ΎΘ§«κ«σ≥ωΒψPΒΡΉχ±ξΘΜ
(3)”–“ΜΗωΒψM¥”ΒψA≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»‘ΎAB…œœρΒψB‘ΥΕ·Θ§Νμ“ΜΗωΒψN¥”ΒψD”κΒψMΆ§ ±≥ωΖΔΘ§“‘ΟΩΟκ2ΗωΒΞΈΜΒΡΥΌΕ»‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ‘ΥΕ·Θ§Β±ΒψMΒΫ ¥οΒψB ±Θ§ΒψMΓΔNΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ§Έ ΒψMΓΔN‘ΥΕ·ΒΫΚΈ¥Π ±Θ§ΓςMNBΟφΜΐΉν¥σΘ§ ‘«σ≥ωΉν¥σΟφΜΐ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§“―÷ΣΕΰ¥ΈΚ· ΐy=-x2+bx+cΒΡΆΦœώ”κx÷αΒΡΫΜΒψΈΣΒψA(3Θ§0)ΚΆΒψBΘ§”κy÷αΫΜ”ΎΒψC(0Θ§3)Θ§Ν§Ϋ”AC.
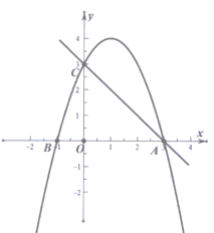
Θ®1Θ©«σ’βΗωΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©‘Ύ(1)÷–ΈΜ”ΎΒΎ“ΜœσœόΡΎΒΡ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψDΘ§ ΙΒΟΓςACDΒΡΟφΜΐΉν¥σ?»τ¥φ‘ΎΘ§«σ≥ωΒψDΒΡΉχ±ξΦΑΓςACDΟφΜΐΒΡΉν¥σ÷ΒΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
Θ®3Θ©‘Ύ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψEΘ§ ΙΒΟΓςACE «“‘ACΈΣ÷±Ϋ«±ΏΒΡ÷±Ϋ«»ΐΫ«–Έ»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψEΒΡΉχ±ξΦ¥Ω…ΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§ΒψD‘ΎABΒΡ―”≥ΛœΏ…œΘ§CΓΔE «Γ―O…œΒΡΝΫΒψΘ§CE=CBΘ§ΓœBCD=ΓœCAEΘ§―”≥ΛAEΫΜBCΒΡ―”≥ΛœΏ”ΎΒψFΘ°
Θ®1Θ©«σ÷ΛΘΚCD «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©«σ÷ΛΘΚCE=CFΘΜ
Θ®3Θ©»τBD=1Θ§CD=![]() Θ§«σœ“ACΒΡ≥ΛΘ°
Θ§«σœ“ACΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
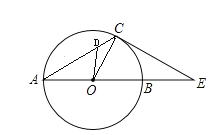
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςACE÷–Θ§CAΘΫCEΘ§ΓœCAEΘΫ30ΓψΘ§Γ―OΨ≠ΙΐΒψCΘ§«“‘≤ΒΡ÷±ΨΕAB‘ΎœΏΕΈAE…œΘ°ΒψD «œΏΕΈAC…œ»Έ“β“ΜΒψΘ®≤ΜΚ§ΕΥΒψΘ©Θ§Ν§Ϋ”ODΘ§Β±ABΘΫ4 ±Θ§‘ρ![]() CD+ODΒΡΉν–Γ÷Β «______Θ°
CD+ODΒΡΉν–Γ÷Β «______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
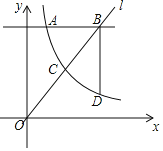
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ζ¥±»άΐΚ· ΐyΘΫ![]() Θ®xΘΨ0Θ©ΒΡΆΦœσ”κ÷±œΏyΘΫmxΫΜ”ΎΒψCΘ§÷±œΏlΘΚyΘΫ4Ζ÷±πΫΜΝΫΚ· ΐΆΦœσ”ΎΒψAΘ®1Θ§4Θ©ΚΆΒψBΘ§ΙΐΒψBΉςBDΓΆlΫΜΖ¥±»άΐΚ· ΐΆΦœσ”ΎΒψ DΘ°
Θ®xΘΨ0Θ©ΒΡΆΦœσ”κ÷±œΏyΘΫmxΫΜ”ΎΒψCΘ§÷±œΏlΘΚyΘΫ4Ζ÷±πΫΜΝΫΚ· ΐΆΦœσ”ΎΒψAΘ®1Θ§4Θ©ΚΆΒψBΘ§ΙΐΒψBΉςBDΓΆlΫΜΖ¥±»άΐΚ· ΐΆΦœσ”ΎΒψ DΘ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±BDΘΫ2AB ±Θ§«σΒψBΒΡΉχ±ξΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§÷±Ϋ”–¥≥ω≤ΜΒ» Ϋ![]() ΘΨmxΒΡΫβΦ·Θ°
ΘΨmxΒΡΫβΦ·Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
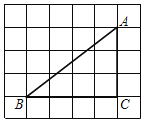
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ6ΓΝ5ΒΡΆχΗώΘ®–Γ’ΐΖΫ–Έ±Ώ≥ΛΈΣ1Θ©÷–Θ§RtΓςABCΒΡ»ΐΗωΕΞΒψΕΦ‘ΎΗώΒψ…œΘ°
Θ®1Θ©‘ΎΆχΗώ÷–Θ§’“ΒΫΗώΒψDΘ§ ΙΥΡ±Ώ–ΈACBDΒΡΟφΜΐΈΣ10Θ§≤ΔΜ≠≥ω’βΗωΥΡ±Ώ–ΈΘ°
Θ®2Θ©Ϋη÷ζΆχΗώΓΔ÷Μ”Ο÷±≥ΏΘ®ΈόΩΧΕ»Θ©‘ΎAB…œ’““ΜΒψEΘ§ ΙΓςAECΈΣΒ»―ϋ»ΐΫ«–ΈΘ§«“AEΘΫACΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ![]() «“ΜΗωΝά“¬ΦήΒΡ ΒΈοΆΦΘ§÷ßΦήΒΡΜυ±ΨΆΦ–Έ «Νβ–ΈΘ§MN «Νά“¬ΦήΒΡ“ΜΗωΜ§≤έΘ§ΒψP‘ΎΜ§≤έMN…œΓΔœ¬“ΤΕ· ±Θ§Νά“¬ΦήΩ…“‘…λΥθΘ§Τδ Ψ“βΆΦ»γΆΦ
«“ΜΗωΝά“¬ΦήΒΡ ΒΈοΆΦΘ§÷ßΦήΒΡΜυ±ΨΆΦ–Έ «Νβ–ΈΘ§MN «Νά“¬ΦήΒΡ“ΜΗωΜ§≤έΘ§ΒψP‘ΎΜ§≤έMN…œΓΔœ¬“ΤΕ· ±Θ§Νά“¬ΦήΩ…“‘…λΥθΘ§Τδ Ψ“βΆΦ»γΆΦ![]() Υυ ΨΘ§“―÷ΣΟΩΗωΝβ–ΈΒΡ±Ώ≥ΛΨυΈΣ20cmΘ§«“
Υυ ΨΘ§“―÷ΣΟΩΗωΝβ–ΈΒΡ±Ώ≥ΛΨυΈΣ20cmΘ§«“![]() Θ°
Θ°

![]() Β±ΒψPœρœ¬Μ§÷ΝΒψN¥Π ±Θ§≤βΒΟ
Β±ΒψPœρœ¬Μ§÷ΝΒψN¥Π ±Θ§≤βΒΟ![]() ±
±
![]() «σΜ§≤έMNΒΡ≥ΛΕ»ΘΜ
«σΜ§≤έMNΒΡ≥ΛΕ»ΘΜ
![]() ¥Υ ±ΒψAΒΫ÷±œΏDPΒΡΨύάκ «Εύ…ΌΘΩ
¥Υ ±ΒψAΒΫ÷±œΏDPΒΡΨύάκ «Εύ…ΌΘΩ
![]() Β±ΒψPœρ…œΜ§÷ΝΒψM¥Π ±Θ§ΒψA‘ΎœύΕ‘”Ύ
Β±ΒψPœρ…œΜ§÷ΝΒψM¥Π ±Θ§ΒψA‘ΎœύΕ‘”Ύ![]() ΒΡ«ιΩωœ¬œρΉσ“ΤΕ·ΒΡΨύάκ «Εύ…ΌΘΩ
ΒΡ«ιΩωœ¬œρΉσ“ΤΕ·ΒΡΨύάκ «Εύ…ΌΘΩ
![]() ΫαΙϊΨΪ»ΖΒΫ
ΫαΙϊΨΪ»ΖΒΫ![]() Θ§≤ΈΩΦ ΐΨί
Θ§≤ΈΩΦ ΐΨί![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com