
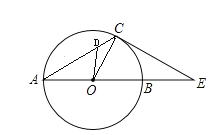
【题目】如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.点D是线段AC上任意一点(不含端点),连接OD,当AB=4时,则![]() CD+OD的最小值是______.
CD+OD的最小值是______.
【答案】![]()
【解析】
作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,易证四边形AOCF是菱形,根据对称性可得DF=DO.过点D作DH⊥OC于H,易得DH=![]() DC,从而有
DC,从而有![]() CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即
CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即![]() CD+OD)最小,然后在Rt△OHF中运用三角函数即可解决问题.
CD+OD)最小,然后在Rt△OHF中运用三角函数即可解决问题.
解:作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图所示,
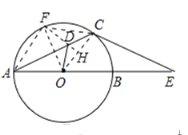
∵OA=OC,∴∠OCA=∠OAC=30°,∴∠COB=60°,
则∠AOF=∠COF=![]() ∠AOC=
∠AOC=![]() (180°-60°)=60°.
(180°-60°)=60°.
∵OA=OF=OC,
∴△AOF、△COF是等边三角形,
∴AF=AO=OC=FC,
∴四边形AOCF是菱形,
∴根据对称性可得DF=DO.
过点D作DH⊥OC于H,
则DH=DCsin∠DCH=DCsin30°=![]() DC,
DC,
∴![]() CD+OD=DH+FD.
CD+OD=DH+FD.
根据两点之间线段最短可得,
当F、D、H三点共线时,DH+FD(即![]() CD+OD)最小,
CD+OD)最小,
∵OF=OA=![]() AB=2,
AB=2,
∴此时FH=DH+FD=OFsin∠FOH=![]() ×2=
×2=![]() ,
,
即![]() CD+OD的最小值为
CD+OD的最小值为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】近些年来,“校园安全”受到全社会的广泛关注,为了了解学生对于安全知识的了解程度,学校采用随机抽样的调查方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.
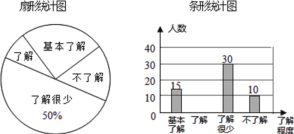
请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有________人.
(2)请补全条形统计图;
(3)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=![]() ,求tanC的值;
,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=![]() ,
,![]() ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.
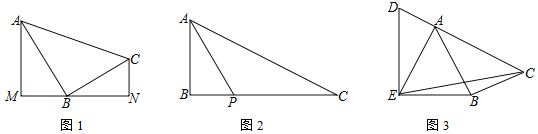
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.已知:在矩形![]() 中,
中,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ;
;
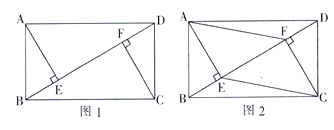
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,连接
时,连接![]() .
.![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
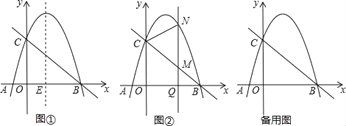
【题目】如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;
(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;
(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
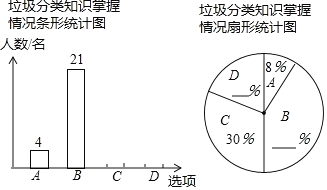
【题目】为响应市政府关于“垃圾不落地市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B:比较了解,C:了解较少,D:不了解”四种,并将调查结果绘制成两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生有2000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有 名;
(3)已知“非常了解”的同学有3名男生和1名女生,从中随机抽取2名进行垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
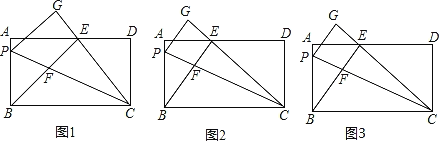
【题目】在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.
(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;
(2)如图2,当AD=25,且AE<DE时,求![]() 的值;
的值;
(3)如图3,当BEEF=108时,求BP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若三角形的一条角平分线与被平分的角的一边相等,则称这个三角形为“弱等腰三角形”,这条角平分线叫做这个三角形的“弱线”,如图①,AD是△ABC的角平分线,当AD=AB时,则△ABC是“弱等腰三角形”,线段AD是△ABC的“弱线”.
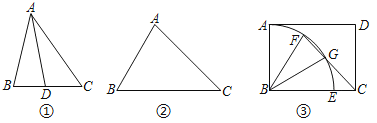
(1)如图②,在△ABC中.∠B=60°,∠C=45°.求证:△ABC是“弱等腰三角形”;
(2)如图③,在矩形ABCD中,AB=3,BC=4.以B为圆心在矩形内部作![]() ,交BC于点E,点F是
,交BC于点E,点F是![]() 上一点,连结CF.且CF与
上一点,连结CF.且CF与![]() 有另一个交点G.连结BG.当BG是△BCF的“弱线”时,求CG的长.
有另一个交点G.连结BG.当BG是△BCF的“弱线”时,求CG的长.
(3)已知△ABC是“弱等腰三角形”,AD是“弱线”,且AB=3BD,求AC:BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班学生做“用频率估计概率”的实验时,给出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
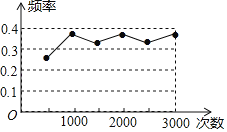
A.抛一枚硬币,出现正面朝上
B.从标有1,2,3,4,5,6的六张卡片中任抽一张,出现偶数
C.从一个装有6个红球和3个黑球的袋子中任取一球,取到的是黑球
D.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com