练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，某海防哨所发现在它的北偏西，距离为的处有一艘船，该船向正东方向航行，经过到达哨所东北方向的处，则该船的航速为每小时___．（精确到）

    【答案】

    【解析】

    设AB与正北方向线交于点C，根据已知及三角函数求得AC、OC的长，再根据等腰直角三角形的性质求得BC的长，利用AB=AC+BC求出AB的长，再除以该船航行的时间即可求解．

    设AB与正北方向线交于点C，

    ∵在直角△AOC中，∠AOC=30°，OA=500米，

    ∴AC=OAsin30°=250米，OC=OAcos30°=250米，

    ∵直角△OBC是等腰直角三角形，

    ∴BC=OC=250米，

    ∴AB=AC+BC=250+250（米），

    ∴该船的航速为=5+5≈13.7（千米/时），

    即该船的航速约为每小时13.7千米．

    故答案为13.7．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（　　）

    A. 4B. 3C. 2D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2011山东济南，27，9分）如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过A、C两点，与AB边交于点D．

    （1）求抛物线的函数表达式；

    （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．

    ①求S关于m的函数表达式，并求出m为何值时，S取得最大值；

    ②当S最大时，在抛物线的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】元旦放假期间，小明和小华准备到西安的大雁塔（记为A）、白鹿原（记为B）、兴庆公园（记为C）、秦岭国家植物园（记为D）中的一个景点去游玩，他们各自在这四个景点中任选一个，每个景点被选中的可能性相同

    （1）求小明选择去白鹿原游玩的概率；

    （2）用树状图或列表的方法求小明和小华选择去同一个地方游玩的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC，按以下步骤作图：①分别以 B，C 为圆心，以大于BC 的长为半径作弧，两弧相交于两点 M，N；②作直线 MN 交 AB 于点 D，连接 CD．若 CD=AC，∠A=50°，则∠ACB 的度数为

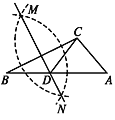
    A.90°B.95°C.105°D.110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有5张背面看上去无差别的扑克牌，正面分别写着5，6，7，8，9，洗匀后正面向下放在桌子上，从中随机抽取2张，抽出的卡片上的数字恰好是两个连续整数的概率是__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某教育局组织了“落实十九大精神，立足岗位见行动”教师演讲比赛，根据各校初赛成绩在小学组、中学组分别选出10名教师参加决赛，这些选手的决赛成绩如图所示：

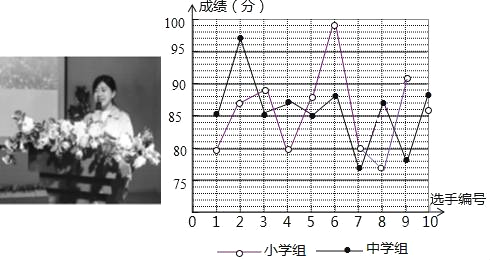
    根据上图提供的信息，回答下列问题：

    （1）请你把下面表格填写完整：

    团体成绩

    众数

    平均数

    方差

    小学组

    　　

    85.7

    39.6

    中学组

    85

    　　

    27.8

    （2）考虑平均数与方差，你认为哪个组的团体成绩更好些，并说明理由；

    （3）若在每组的决赛选手中分别选出3人参加总决赛，你认为哪个组获胜的可能性大些？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是等边三角形，点D是BC边上一动点，点E，F分别在AB，AC边上，连接AD，DE，DF，且∠ADE=∠ADF=60°．

    小明通过观察、实验，提出猜想：在点D运动的过程中，始终有AE=AF，小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

    想法1：利用AD是∠EDF的角平分线，构造△ADF的全等三角形，然后通过等腰三角形的相关知识获证．

    想法2：利用AD是∠EDF的角平分线，构造角平分线的性质定理的基本图形，然后通过全等三角形的相关知识获证．

    想法3：将△ACD绕点A顺时针旋转至△ABG，使得AC和AB重合，然后通过全等三角形的相关知识获证．

    请你参考上面的想法，帮助小明证明AE=AF．（一种方法即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

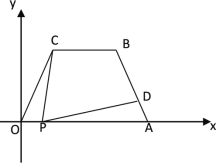
    【题目】如图所示，在平面直角坐标中，四边形OABC是梯形，且AB = OC = 4，CB∥OA，OA = 7，∠COA = 60°，点P为x轴上的—个动点，点P不与点0、点A重合．连结CP，过点P作PD交AB于点D，

    （1）求点B的坐标；

    （2）当点P运动什么位置时，使得∠CPD =∠OAB，且，求这时点P的坐标；

    （3）当点P运动什么位置时，△OCP为等腰三角形，直接写出这时点P的坐标。

    查看答案和解析>>

    同步练习册答案