
【题目】已知抛物线C:y1=ax2-ah(2x-h)-2,直线l:y2=k(x-h)-2.
(1)求证:直线l恒过抛物线C的顶点;
(2)当a=-1,m≤x≤2时,y1≥x-4恒成立,求m的最小值;
(3)当0<a≤3,k>0时,若在直线l下方的抛物线C上至少存在两个横坐标为整数的点,求k的取值范围.
【答案】(1)证明见解析;(2)1;(3)k>6.
【解析】
(1)由抛物线的解析式可知抛物线的顶点坐标为(h,-2),然后证明点(h,-2)符合直线y2=k(x-h)-2的解析式即可;
(2)令![]() ,依据拋物线的解析式可得到拋物线的顶点在直线y=-2上,由m≤x≤2时,y1≥x-4恒成立可得到拋物线的顶点坐标为(2,-2),然后找出抛物线y1=ax2-ah(2x-h)-2位于直线
,依据拋物线的解析式可得到拋物线的顶点在直线y=-2上,由m≤x≤2时,y1≥x-4恒成立可得到拋物线的顶点坐标为(2,-2),然后找出抛物线y1=ax2-ah(2x-h)-2位于直线![]() 上方时自变量x的取值范围,从而可确定出m的最小值;
上方时自变量x的取值范围,从而可确定出m的最小值;
(3)由(1)可知抛物线C与直线l都过点A(h,-2).当0<a≤3时,k>0,在直线l下方的抛物线C上至少存在两个横坐标为整数点,即当x=h+2时,![]() 恒成立,然后由
恒成立,然后由![]() 可得到关于k的不等式,从而可求得k:的取值范围.
可得到关于k的不等式,从而可求得k:的取值范围.
解:(1)y1=ax2-ah(2x-h)-2=![]()
抛物线C的顶点坐标为(h,-2),当x=h时,y2=k(h-h)-2=-2,所以直线l恒过抛物线C的顶点(h,-2);
(2)当a=-1时,抛物线C解析式为y1=![]() ,令
,令![]() 如图所示:
如图所示:
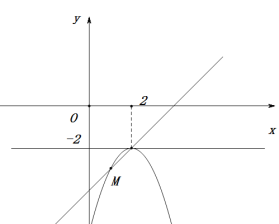
抛物线C的顶点在直线y=-2上移动,图1当m≤x≤2时,y1≥x-4恒成立,则可知抛物线C的顶点为(2,-2),设抛物线C与直线![]() 除顶点外的另一交点为M,此时点M的横坐标即为m的最小值,由
除顶点外的另一交点为M,此时点M的横坐标即为m的最小值,由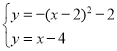 ,解得
,解得![]() ,所以m的最小值为1.
,所以m的最小值为1.
(3)如图2所示:由(1)可知:抛物线C与直线l都过点A(h,-2).如图所示:
当0<a≤3时,k>0,在直线l下方的抛物线C上至少存在两个横坐标为整数点,即当x=h+2时,![]() 恒成立.
恒成立.
所以![]() ,整理得:得:k>2a.又因为0<a≤3,所以0<2a<6,所以k>6.
,整理得:得:k>2a.又因为0<a≤3,所以0<2a<6,所以k>6.
分析:


科目:初中数学 来源: 题型:
【题目】小明放学回家看到桌上有一盘小麻糕,妈妈说当中有芝麻馅、肉馅各1个,青菜馅2个,这些小麻糕除馅外无其他差别.
(1)小明随机从盘中取出一个小麻糕,取出的是芝麻馅的概率是_________.
(2)小明随机从盘中一次取出两个小麻糕,试用画树状图或列表的方法表示所有可能的结果,并求取出的两个都是青菜馅的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.天气预报说明天降水的概率为 10%,则明天一定是晴天
B.任意抛掷一枚均匀的 1 元硬币,若上一次正面朝上,则下一次一定反面朝上
C.13 人中至少有 2 人的出生月份相同
D.任意抛掷一枚均匀的骰子,掷出的点数小于3 的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() x2﹣x+m的图象经过点A(1,﹣2)
x2﹣x+m的图象经过点A(1,﹣2)
(1)求此函数图像与坐标轴的交点坐标;
(2)若P(-2,y1),Q(5,y2)两点在此函数图像上,试比较y1,y2的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚棋子放在边长为1个单位长度的正六边形

ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在
一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀
后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1
个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位
长度.
棋子走到哪一点的可能性最大?求出棋子走到该点的概率.(用列表或画树状图的方法
求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了本校九年级300名学生到校的方式,根据调査结果绘制出统计图的一部分如图:
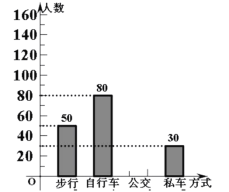
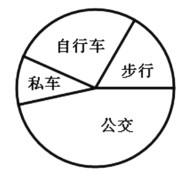
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)请估计在全校1200名学生中乘公交的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC、AB相交于点D、E,连接AD,已知∠CAD=∠B.
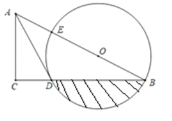
(1)求证:AD是⊙O的切线;
(2)若∠B=30°,AC=![]() ,求劣弧BD与弦BD所围阴影图形的面积;
,求劣弧BD与弦BD所围阴影图形的面积;
(3)若AC=4,BD=6,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线y=x2+bx+c与直线y=﹣x﹣1交于点A,B.其中点B的横坐标为2.点P(m,n)是线段AB上的动点.
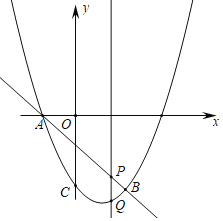
(1)求抛物线的表达式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平角直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形,在(2)的情况下,在平面内找出所有符合要求的整点R,使P、Q、B、R为整点平行四边形,请直接写出整点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com