
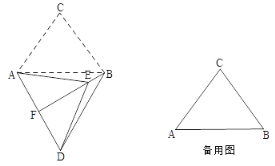
����Ŀ����ͼ1����CΪ�߶�AB������һ�㣨�����A��B�غϣ����ֱ���AC��BCΪһ����AB��ͬ����������ACD�͡�BCE��CA��CD��CB��CE����ACD����BCE��30�㣬����AE��CD�ڵ�M������BD��CE�ڵ�N��AE��BD���ڵ�P������CP��
��1���߶�AE��DB��������ϵΪ�� ����ֱ��д����APD���� ��
��2������BCE�Ƶ�C��ת����ͼ2��ʾ��λ�ã������������䣬̽���߶�AE��DB��������ϵ����˵�����ɣ������ʱ��APD�Ķ�����
��3���ڣ�2������������֤����APC����BPC��

���𰸡���1��AE��BD��30�㣻��2�����ۣ�AE��BD����APD��30�㣮���ɼ���������3��������.
��������
��1��ֻҪ֤����ACE�ա�DCB�����ɽ�����⣻
��2��ֻҪ֤����ACE�ա�DCB�����ɽ�����⣻
��3����ͼ2-1�У��ֱ��C��CH��AE������ΪH������C��CG��BD������ΪG�����������֤��CG=CH�������ý�ƽ���ߵ��ж�����֤����DPC=��EPC���ɽ�����⣻
��1���⣺��ͼ1�У�
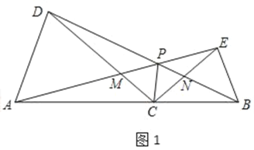
�ߡ�ACD����BCE��
���ACD+��DCE����BCE+��DCE��
���ACE����DCB��
�֡�CA��CD��CE��CB��
���ACE�ա�DCB��
��AE��BD����CAE����CDB��
�ߡ�AMC����DMP��
���APD����ACD��30����
�ʴ�ΪAE��BD��30��
��2����ͼ2�У����ۣ�AE��BD����APD��30����
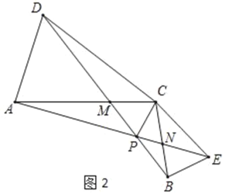
���ɣ��ߡ�ACD����BCE��
���ACD+��DCE����BCE+��DCE��
���ACE����DCB��
�֡�CA��CD��CE��CB��
���ACE�ա�DCB��
��AE��BD����CAE����CDB��
�ߡ�AMP����DMC��
���APD����ACD��30����
��3����ͼ2��1�У��ֱ��C��CH��AE������ΪH������C��CG��BD������ΪG��

�ߡ�ACE�ա�DCB��
��AE��BD��
��S��ACE��S��DCB
��CH��CG��
���DPC����EPC
�ߡ�APD����BPE��
���APC����BPC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���廳���ң��̳���־��ij��ѧ�����꼶ͬѧ��4�³��������������ܺ��������ҹ����������Ķ���ԽҰ�ÿ��С����Ҫ�ڵ�![]() �������ܲ�����
�������ܲ�����![]() ��ÿС���ʱ��Ϊ1���ӣ���Ȼ���ܲ���
��ÿС���ʱ��Ϊ1���ӣ���Ȼ���ܲ���![]() �㣬��������յ㣨�����
�㣬��������յ㣨�����![]() ����
����![]() ����
����![]() ��һ��ֱ���ϣ������н������У�ÿ��С���ܲ��ٶ��Dz���ģ����������������ȳ���������һ��ʱ���������������ʼ����������С��ǡ��ͬʱ�����
��һ��ֱ���ϣ������н������У�ÿ��С���ܲ��ٶ��Dz���ģ����������������ȳ���������һ��ʱ���������������ʼ����������С��ǡ��ͬʱ�����![]() ��������������������ʱ��Ϊ
��������������������ʱ��Ϊ![]() ����λ�����ӣ����ڵ�
����λ�����ӣ����ڵ�![]() ���
���![]() ֮����н������У�����������������������֮��ľ���Ϊ
֮����н������У�����������������������֮��ľ���Ϊ![]() ����λ���ף������ǵĺ���ͼ������ͼ���������жϲ���ȷ���ǣ� ��
����λ���ף������ǵĺ���ͼ������ͼ���������жϲ���ȷ���ǣ� ��
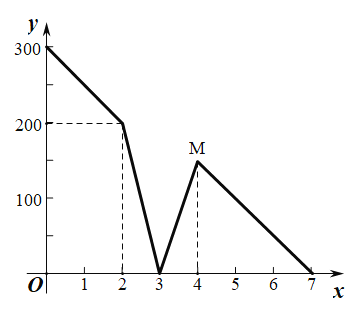
A.��![]() ʱ������������ǡ�õ���
ʱ������������ǡ�õ���![]() �㣻
�㣻
B.�������������ٶ�Ϊ150��/���ӣ��������������ٶ�Ϊ200��/�������Ǵ�![]() �������ʱ����Ϊ2����
�������ʱ����Ϊ2����
C.ͼ��![]() ���ʾ������������
���ʾ������������![]() ���������ʼ��
���������ʼ��![]() �������
�������
D.������![]() ����
����![]() �ľ�����600�ף���
�ľ�����600�ף���![]() ����
����![]() �ľ�����800��
�ľ�����800��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
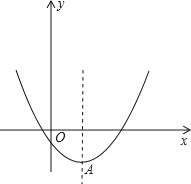
����Ŀ����֪���κ���y=x2��2mx+4m��8,
��1����x��2ʱ������ֵy��x���������С����m��ȡֵ��Χ��
��2����������y=x2��2mx+4m��8�Ķ���AΪһ���������������ߵ��ڽ���������AMN��M��N�����ڒ������ϣ������ʣ���AMN���������m�صĶ�ֵ�����ǣ�����������ֵ�������ǣ���˵�����ɣ�
��3����������y=x2��2mx+4m��8��x�ύ��ĺ������Ϊ������������m����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1����3ab��2����![]() ab3��
ab3��
��2��20182��2016��2020�����ó˷���ʽ���㣩
��3����12019+����![]() ����2+
����2+![]() ��������3.14��0
��������3.14��0
��4��[2��x+2y��2����x+y����4x��y����9y2]������2x��������x����2��y��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB��12��AC��BC��10������ABC�Ƶ�A��˳ʱ�뷽����ת���õ���ADE����ת��Ϊ��(0��<��<180��)����B�Ķ�Ӧ��ΪD����C�Ķ�Ӧ��ΪE������BD��BE��
��1����ͼ��������60��ʱ���ӳ�BE��AD�ڵ�F��
����֤����ABD�ǵȱ������Σ�
����֤��BF��AD��AF��DF��
����ֱ��д��BE�ij���
��2������ת�����У�����D��DG��ֱ��ֱ��AB������ΪG������CE������DAG����ACB�����߶�DG���߶�AE������ʱ����ֱ��д��BE��CE��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˽���![]() �ױ������ڱ��������У��������ܵ�·��
�ױ������ڱ��������У��������ܵ�·��![]() ���ף������õ�ʱ��
���ף������õ�ʱ��![]() ���֣��ĺ�����ϵ��ͼ��ʾ��������˵�����ټ��ȵ����յ㣻����ɱ������ұȼ�����
���֣��ĺ�����ϵ��ͼ��ʾ��������˵�����ټ��ȵ����յ㣻����ɱ������ұȼ�����![]() �룻�۳���
�룻�۳���![]() ���Ӻ��ұȼ��ٶȿ죻��
���Ӻ��ұȼ��ٶȿ죻��![]() ��ʱ�ס������
��ʱ�ס������![]() �ף����д���ĸ����ǣ� ����
�ף����д���ĸ����ǣ� ����

A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ������ƽ���ڣ�������y=x2+bx+c������A��2��0����B��0��6����
��1���������ߵı���ʽ��
��2������������ƽ�Ƽ�����λ���㣨4��0������ͨ������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ8��B��������λ�ڵ�A���һ�㣬��AB=22������P��A���������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
��1���������ϵ�B��ʾ������������P��ʾ�����������ú�t�Ĵ���ʽ��ʾ��
��2������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʶ�����ʱP��Q֮��ľ���ǡ�õ���2��
��3������Q�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Qͬʱ�������ʵ�P�˶�������ʱ�ϵ�Q��
��4����MΪAP���е㣬NΪBP���е㣬�ڵ�P�˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ԫһ�η�����![]() �Ľ� x��y ��ֵ��һ���������������ߵij�����������������ε��ܳ�Ϊ 5�������ij�����ע����������������ȵ������߽������������ε�����
�Ľ� x��y ��ֵ��һ���������������ߵij�����������������ε��ܳ�Ϊ 5�������ij�����ע����������������ȵ������߽������������ε�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com