
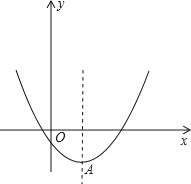
【题目】已知二次函数y=x2﹣2mx+4m﹣8,
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
【答案】(1)m≥2;(2)△AMN是边长为2![]() 的正三角形,S△AMN=3
的正三角形,S△AMN=3![]() ,与m无关;(3)m=2.
,与m无关;(3)m=2.
【解析】试题分析:(1)求出二次函数的对称轴x=m,由于抛物线的开口向上,在对称轴的左边y随x的增大而减小,可以求出m的取值范围.
(2)在抛物线内作出正三角形,求出正三角形的边长,然后计算三角形的面积,得到△AMN的面积是m无关的定值.
(3)当y=0时,求出抛物线与x轴的两个交点的坐标,然后确定整数m的值.
试题解析:(1)二次函数y=x2-2mx+4m-8的对称轴是:x=m.
∵当x≤2时,函数值y随x的增大而减小,
而x≤2应在对称轴的左边,
∴m≥2.
(2)如图:顶点A的坐标为(m,-m2+4m-8)
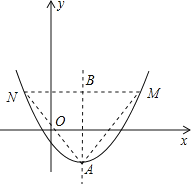
△AMN是抛物线的内接正三角形,
MN交对称轴于点B,tan∠AMB=tan60°=![]() ,
,
则AB=![]() BM=
BM=![]() BN,
BN,
设BM=BN=a,则AB=![]() a,
a,
∴点M的坐标为(m+a, ![]() a-m2+4m-8),
a-m2+4m-8),
∵点M在抛物线上,
∴![]() a-m2+4m-8=(m+a)2-2m(m+a)+4m-8,
a-m2+4m-8=(m+a)2-2m(m+a)+4m-8,
整理得:a2-![]() a=0
a=0
得:a=![]() (a=0舍去)
(a=0舍去)
所以△AMN是边长为2![]() 的正三角形,
的正三角形,
S△AMN=![]() ×2
×2![]() ×3=3
×3=3![]() ,与m无关;
,与m无关;
(3)当y=0时,x2-2mx+4m-8=0,
解得:![]() ,
,
∵抛物线y=x2-2mx+4m-8与x轴交点的横坐标均为整数,
∴(m-2)2+4应是完全平方数,
∴m的最小值为:m=2.
考点: 二次函数综合题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB=6,OC=5.点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线![]() 与y轴平行,直线
与y轴平行,直线![]() 交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线
交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线![]() 恰好过点C.
恰好过点C.
(1)求点A和点B的坐标;
(2)当0<t<3时,求m关于t的函数关系式;
(3)当m=3.5时,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条平行直线上各有![]() 个点,用这
个点,用这![]() 对点按如下的规则连接线段:①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;②符合①要求的线段必须全部画出;图1展示了当
对点按如下的规则连接线段:①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;②符合①要求的线段必须全部画出;图1展示了当![]() 时的情况,此时图中三角形的个数为0;图2展示了当
时的情况,此时图中三角形的个数为0;图2展示了当![]() 时的一种情况,此时图中三角形的个数为2;图3展示了当
时的一种情况,此时图中三角形的个数为2;图3展示了当![]() 时的一种情况,此时图中三角形的个数为4;试猜想当
时的一种情况,此时图中三角形的个数为4;试猜想当![]() 时,按照上述规则画出的图形中,三角形最少有____个
时,按照上述规则画出的图形中,三角形最少有____个

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,天星山山脚下西端A处与东端B处相距800(1+![]() )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为![]() 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米)
(参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B的坐标分别为(1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.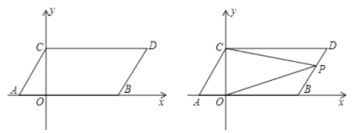
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;
(3)点P是直线BD上一个动点,连接PC、PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD、∠POB的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD=∠BCE=30°,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP.
(1)线段AE与DB的数量关系为 ;请直接写出∠APD= ;
(2)将△BCE绕点C旋转到如图2所示的位置,其他条件不变,探究线段AE与DB的数量关系,并说明理由;求出此时∠APD的度数;
(3)在(2)的条件下求证:∠APC=∠BPC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某建筑物AC上,挂着一宣传条幅BC,站在点F处,测得条幅顶端B的仰角为300,往条幅方向前行20米到达点E处,测得条幅顶端B的仰角为600,求宣传条幅BC的长.(![]() ,结果精确到0.1米)
,结果精确到0.1米)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com