
分析 要求实数b的值,根据题意可知,b存在两种情况,分别画出相应的图形,然后进行推导,即可得到b的值,本题得以解决.
解答 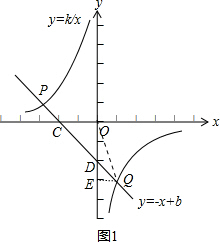 解:当b<0时,作QE⊥y轴于点E,连接OQ,如右图1所示,
解:当b<0时,作QE⊥y轴于点E,连接OQ,如右图1所示,
∵直线y=-x+b(b≠0),与x轴、y轴分别相交于C、D两点,
∴当x=0时,y=b;当y=0时,x=b;
即点C的坐标是(b,0),点D的坐标是(0,b),
∴OC=OD=-b,
∵S△ODQ=S△OCD,
∴$\frac{OC•OD}{2}=\frac{OD•QE}{2}$,
∴OC=QE,
∴点Q的坐标是(-b,2b),
∵反比例函数y=$\frac{k}{x}$的图象经过点A(-1,4),
∴$4=\frac{k}{-1}$,得k=-4,
∴$y=\frac{-4}{x}$,
又∵点Q(-b,2b)在$y=\frac{-4}{x}$上,
∴$2b=\frac{-4}{-b}$,
解得,b=-$\sqrt{2}$或b=$\sqrt{2}$(舍去);
当b>0时,如右图2所示,
此时△ODQ与△OCD的面积不相等,故不符合题意;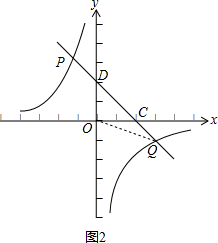 故答案为:$-\sqrt{2}$.
故答案为:$-\sqrt{2}$.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,画出相应的图形,利用数形结合的思想解答问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
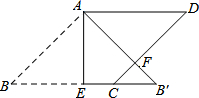 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2$-\sqrt{2}$ | D. | 2$\sqrt{2}$-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
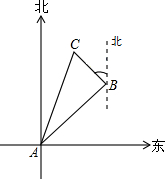 如图,在一次实践活动中,小强从A地出发,沿北偏东60°的方向行进3$\sqrt{3}$千米到达B地,然后再沿北偏西30°方向行进了3千米到达目的地C.
如图,在一次实践活动中,小强从A地出发,沿北偏东60°的方向行进3$\sqrt{3}$千米到达B地,然后再沿北偏西30°方向行进了3千米到达目的地C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学生的视力状况受到社会的普遍关注,某校为了解学生的视力情况,对本校学生的视力情况进行了抽样调查,并对调查结果进行了整理,制成了所示的统计图标(不完整),x表示视力情况.根据所提供的信息,解答下列问题:
学生的视力状况受到社会的普遍关注,某校为了解学生的视力情况,对本校学生的视力情况进行了抽样调查,并对调查结果进行了整理,制成了所示的统计图标(不完整),x表示视力情况.根据所提供的信息,解答下列问题:| 分组 | 视力情况 | 频数 | 频率 |
| A | x<4.1 | 20 | 0.10 |
| B | 4.1≤x<4.5 | 70 | 0.35 |
| C | 4.5≤x<4.9 | 50 | 0.25 |
| D | x≥4.9 | 60 | 0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
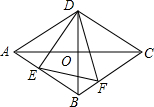 如图,菱形ABCD,点E是边AB上一点,点F在BC上,AB=4,∠ABC=120°,在以下四个结论中,正确的是①②③.
如图,菱形ABCD,点E是边AB上一点,点F在BC上,AB=4,∠ABC=120°,在以下四个结论中,正确的是①②③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com