
���� ��1����A���B������ֱ����y=x2+bx+c�ù���b��c�ķ����飬Ȼ��ⷽ�������b��c���ɣ�
��2����ͨ���ⷽ��x2-2x-3=0�ɵ�D�����꣬Ȼ����������ʽ�õ�$\frac{1}{2}$��3����m+1��=$\frac{21}{4}$���ٽ����m�ķ��̼��ɣ�
�����������ߵ�ƽ�Ʊ任������������C2�Ľ���ʽΪy=��x-1��2-4+n�����ۣ��ֱ����������C2����E��ԭ��ʱ��Ӧ��n��ֵ�����һ�������ͼ�����ú���ͼ���ȷ��n�ķ�Χ����������C2�Ķ�����x���ϣ���n=4����ʱ��������������Ȼ���ۺ�����������ɵõ�n��ȡֵ��Χ��
��� �⣺��1����A��2��-3����B��3��0������y=x2+bx+c��$\left\{\begin{array}{l}{4+2b+c=-3}\\{9+3b+c=0}\end{array}\right.$�����$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$��
���������ߵĽ���ʽΪy=x2-2x-3��
��2���ٵ�y=0ʱ��x2-2x-3=0�����x1=-1��x2=3����D��-1��0����
�ߡ�ADE�����Ϊ$\frac{21}{4}$��
��$\frac{1}{2}$��3����m+1��=$\frac{21}{4}$��
��m=$\frac{5}{2}$��
�ڡ�������C1�Ľ���ʽΪy=��x-1��2-4��
��������C2�Ľ���ʽΪy=��x-1��2-4+n��
��������C2������E��$\frac{5}{2}$��0��ʱ����$\frac{5}{2}$-1��2-4+n=0�����n=$\frac{7}{4}$��
��������C2�����㣨0��0��ʱ����0-1��2-4+n=0�����n=3��
�ߵ�0��x��$\frac{5}{2}$ʱ��������C2��x��ֻ��һ�������㣬
����ͼ��ɵ�$\frac{7}{4}$��n��3ʱ������������
��������C2�Ķ�����x���ϣ���n=4����ʱ��������Ϊ��1��4��������������
����������n��ȡֵ��ΧΪn=4��$\frac{7}{4}$��n��3��
���� ���⿼���˶��κ�����x��Ľ��㣺������κ���y=ax2+bx+c��a��b��c�dz�����a��0����x��Ľ������껯Ϊ�����x��һԪ���η��̣����ڶ��κ���y=ax2+bx+c��a��b��c�dz�����a��0������=b2-4ac������������x��Ľ����������=b2-4ac��0ʱ����������x����2�����㣻��=b2-4ac=0ʱ����������x����1�����㣻��=b2-4ac��0ʱ����������x��û�н��㣮�������ν�ϵ�˼���ǽ����2��С��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | A�䣨3��3����B�䣨0��0�� | B�� | A�䣨-2��-2����B�䣨0��0�� | C�� | A�䣨3��3����B�䣨5��5�� | D�� | A�䣨3��3����B�䣨-5��5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
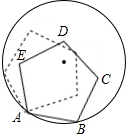 ��ͼ���߳�Ϊ1���������ABCDE������A��B�ڰ뾶Ϊ1��Բ�ϣ�����������Բ�ڣ����������ABCDE�Ƶ�A��ʱ����ת������E��һ������Բ��ʱ�����Cת���Ķ���Ϊ12�㣮
��ͼ���߳�Ϊ1���������ABCDE������A��B�ڰ뾶Ϊ1��Բ�ϣ�����������Բ�ڣ����������ABCDE�Ƶ�A��ʱ����ת������E��һ������Բ��ʱ�����Cת���Ķ���Ϊ12�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com