
【题目】已知,∠AOD=160°,OB、OM、ON 是∠AOD内的射线
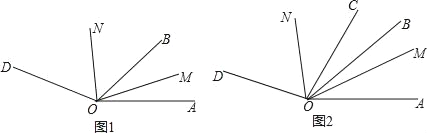
(1)如图1,若OM平分∠AOB,ON平分∠BOD,则∠MON= °
(2)如图2,OC是∠AOD内的射线,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD,当射线OB在∠AOC内时,求∠MON的大小;
(3)如图2,在(2)的条件下,当∠AOB=2t°时,∠AOM:∠DON=2:3,求t的值.
【答案】(1)80(2)70°(3)26
【解析】试题分析:(1)根据角平分线的性质,结合角的和差关系求解即可;
(2)根据题意,设∠AOB=x,则∠BOD=160°﹣x,然后根据角平分线的性质,结合角的和差关系求解即可;
(3)根据由∠AOB=2t°,∠BOC=20°,则∠AOC=2t°+20°,∠BOD=160°﹣2t°,然后根据比例关系列式求解即可.
试题解析:(1)∵OM平分∠AOB,ON平分∠BOD,
∴∠BOM=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=∠BOM+∠BON=![]() (∠AOB+∠BOD),
(∠AOB+∠BOD),
∵∠AOD=∠AOB+∠BOD=160°,
∴∠MON=![]() ×160°=80°;
×160°=80°;
故答案为:80;
(2)设∠AOB=x,则∠BOD=160°﹣x,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=![]() ∠AOC=
∠AOC=![]() (x+20°),∠BON=
(x+20°),∠BON=![]() ∠BOD=
∠BOD=![]() (160°﹣x),
(160°﹣x),
∴∠MON=∠COM+∠BON﹣∠BOC=![]() (x+20°)+
(x+20°)+![]() (160°﹣x)﹣20°=70°;
(160°﹣x)﹣20°=70°;
(3)由∠AOB=2t°,∠BOC=20°,则∠AOC=2t°+20°,∠BOD=160°﹣2t°,
∴∠AOM=![]() ∠AOC=t°+10°,∠DON=
∠AOC=t°+10°,∠DON=![]() ∠BOD=80°﹣t°,
∠BOD=80°﹣t°,
∵∠AOM:∠DON=2:3,
∴![]() =
=![]() ,
,
解得:t=26.


科目:初中数学 来源: 题型:
【题目】在△ABC中∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( ) 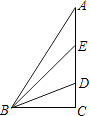
A.BC是△ABE的高
B.BE是△ABD的中线
C.BD是△EBC的角平分线
D.∠ABE=∠EBD=∠DBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0). 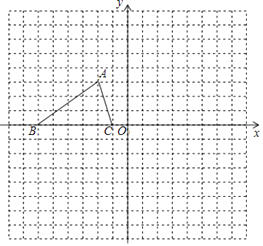
(1)将△ABC沿y轴翻折,则翻折后点A的对应点的坐标是 .
(2)作出△ABC关于y轴对称的图形△A1B1C1 , 画△A1B1C1 , 并直接写出点A1的坐标.
(3)将△ABC向下平移平移6个单位,向右平移7个单位得到△A2B2C2 , 画出平移后的图形.
(4)若以D,B,C为顶点的三角形与△ABC全等,请画出所有符合条件的△DBC(点D与点A重合除外),并直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
一列火车要以每秒20米的速度通过第一、第二两座铁桥(火车的长度忽略不计)过第二座铁桥比过第一座铁桥多50秒,已知铁桥的长度比第一座铁桥的长度的两倍短500米,求两座铁桥各自的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com