
【题目】如图,△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于F,交AB于E,BF=5cm,求CF的长. 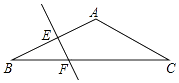
【答案】解:连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF为AB的垂直平分线,
∴AF=BF,
∴∠BAF=∠B=30°,
∴∠FAC=90°,
∵BF=5cm,
∴AF=5cm,
∴FC=10cm.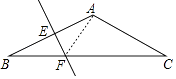
【解析】根据等边对等角可得∠B=∠C=30°,再根据线段垂直平分线的性质可得∠BAF=∠B=30°,进而可得∠FAC=90°,再根据在直角三角形中,30°角所对的直角边等于斜边的一半可得答案.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知,∠AOD=160°,OB、OM、ON 是∠AOD内的射线
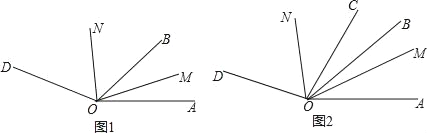
(1)如图1,若OM平分∠AOB,ON平分∠BOD,则∠MON= °
(2)如图2,OC是∠AOD内的射线,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD,当射线OB在∠AOC内时,求∠MON的大小;
(3)如图2,在(2)的条件下,当∠AOB=2t°时,∠AOM:∠DON=2:3,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五月份,邹城八中举行 “做八中发展功臣,为学校发展增光添彩”演讲比赛,将演讲教师的成绩划分为A、B、C、D四个等级,绘制了两种不完整统计图.
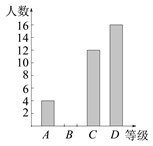

根据图中提供的信息,解答下列问题:
(1)参加演讲比赛的教师共有__________,扇形统计图中m=__________,n=__________,并把条形统计图补充完整.
(2)学校欲从A等级2名男教师2名女女教师中随机选取两人,参加邹城市教育局举办的演讲比赛,请利用列表法或树状图,求A等级中一男一女参加比赛的概率.(男生分别用代码A1、A2表示,女生分别用代码B1、B2表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论正确的是
①P在∠A的平分线上;②QP∥AR;③△BRP≌△QSP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,将一块等腰直角三角板的锐角顶点与A重合,并将三角板绕A点旋转,如图1,使它的斜边与BD交于点H,一条直角边与CD交于点G.
(1)请适当添加辅助线,通过三角形相似,求出![]() 的值;
的值;
(2)连接GH,判断GH与AF的位置关系,并证明;
(3)如图2,将三角板旋转至点F恰好在DC的延长线上时,若AD=![]() ,AF=
,AF=![]() .求DG的长.
.求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=4cm.动点E从点B出发,沿着线路BC→CD→DA运动,在BC段的平均速度是1cm/s,在CD段的平均速度是2cm/s,在DA段的平均速度是4cm/s,到点A停止.设△ABE的面积为y(cm2),则y与点E的运动时间t(s)的函数关系图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com