
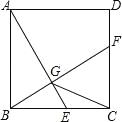
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为![]() -1.其中正确的说法是 .(把你认为正确的说法的序号都填上)
-1.其中正确的说法是 .(把你认为正确的说法的序号都填上)
【答案】②④.
【解析】
试题解析:如图:
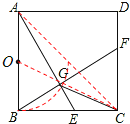
∵在正方形ABCD中,BF⊥AE,
∴∠AGB保持90°不变,
∴G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,
∴当E移动到与C重合时,F点和D点重合,此时G点为AC中点,
∴AG=GE,故①错误;
∵BF⊥AE,
∴∠AEB+∠CBF=90°,
∵∠AEB+∠BAE=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
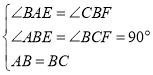 ,
,
∴△ABE≌△BCF(AAS),
∴故②正确;
∵当E点运动到C点时停止,
∴点G运动的轨迹为![]() 圆,
圆,
圆弧的长=![]() ×π×2=
×π×2=![]() ,故③错误;
,故③错误;
由于OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,
OC=![]() ,
,
CG的最小值为OC-OG=![]() -1,故④正确;
-1,故④正确;
综上所述,正确的结论有②④.


科目:初中数学 来源: 题型:
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y=![]() x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
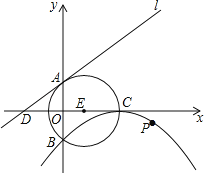
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3) 动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线y=![]() x相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=2时,r2016= .
x相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=2时,r2016= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个口袋,A口袋中装有两个分别标有数字2,3的小球;B口袋中装有三个分别标有数字3,4,5的小球.小明先从A口袋中随机取出-个小球,再从B口袋中随机取出一个小球;
(1)用树状图法或列表法表示小明所取出的二个小球的和为奇数的概率.
(2)若从A口袋中取出的小球记为x,从B口袋中取出的小球记为y,则点M(x,y)落在直线y=x+1上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.根据以上信息,原来报名参加的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD![]() BC=AP
BC=AP![]() BP.
BP.
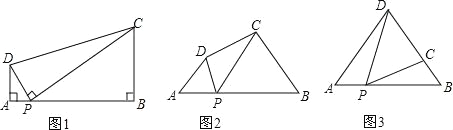
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
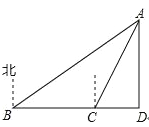
【题目】如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继 续向正东方向航行200海里到达C处时,测得小岛A在船的北偏东30°的方向.己知在小岛周围170海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AD∥BC,AB⊥BC,点E在边AB上,∠DEC=900,且DE=EC.
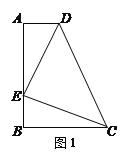

(1)求证:△ADE≌△BEC;
(2)若AD=a,AE=b,DE=c,请用图1证明勾股定理:a2+b2=c2;
(3)线段AB上另有一点F(不与点E重合),且DF⊥CF(如图2),若AD=2,BC=4,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com