
【题目】计算下列各题:
(1)2+(﹣1)=_____.
(2)﹣10+3=_____.
(3)(﹣2)×(﹣3)=_____.
(4)12÷(﹣3)=_____.
(5)(﹣3)2×![]() =_____.
=_____.
(6)1÷5×(![]() )=_____.
)=_____.
(7)﹣3a2+2a2=_____.
(8)﹣2(x﹣1)=_____.
【答案】1 ﹣7 6 ﹣4 5 ﹣![]() ﹣a2 ﹣2x+2
﹣a2 ﹣2x+2
【解析】
(1)直接利用有理数的加减运算法则计算得出答案;
(2)直接利用有理数的加减运算法则计算得出答案;
(3)直接利用有理数的乘除运算法则计算得出答案;
(4)直接利用有理数的乘除运算法则计算得出答案;
(5)直接利用有理数的乘除运算法则计算得出答案;
(6)直接利用有理数的乘除运算法则计算得出答案;
(7)直接合并同类项得出答案;
(8)直接去括号得出答案.
解:(1)2+(﹣1)=1.
(2)﹣10+3=﹣7.
(3)(﹣2)×(﹣3)=6.
(4)12÷(﹣3)=﹣4.
(5)(﹣3)2×![]() =5.
=5.
(6)1÷5×(![]() )=﹣
)=﹣![]() .
.
(7)﹣3a2+2a2=﹣a2.
(8)﹣2(x﹣1)=﹣2x+2.
故答案为:(1)1;(2)﹣7;(3)6;(4)﹣4;
(5)5;(6)﹣![]() ;(7)﹣a2;(8)﹣2x+2.
;(7)﹣a2;(8)﹣2x+2.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )

A. (![]() ,
, ![]() ) B. (
) B. (![]() ,11) C. (2,2
,11) C. (2,2![]() ) D. (
) D. (![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( )
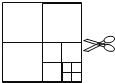
A. 669 B. 670 C. 671 D. 672
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形OABC中,AB∥OC,∠OAB=90°, ∠OCB=60°,AB=2,OA=2![]() .
.
(1)如图①,连接OB,请直接写出OB的长度;
(2)如图②,过点O作OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,设点P运动的时间为t秒,△OPQ的面积为S(平方单位).
①求S与t之间的函数关系式;
②设PQ与OB交于点M,当△OPM为等腰三角形时,试求出△OPQ的面积S的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,则当x=4时,点R应运动到( )

A. P处B. Q处C. M处D. N处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:
①ac>0;②b2﹣4ac>0;③a+c<2﹣b;④a<﹣![]() ;⑤x=﹣5和x=7时函数值相等.
;⑤x=﹣5和x=7时函数值相等.
其中正确的结论有( )
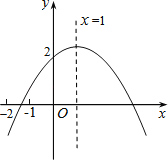
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.

(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人用4张扑克牌(分别是红桃2,红桃3,黑桃4,方片5)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先取一张,取出的牌不放回,乙从剩余的牌中取一张.
(1)设![]() 、
、![]() 分别表示甲、乙取出的牌面上的数字,写出
分别表示甲、乙取出的牌面上的数字,写出![]() 的所有结果;
的所有结果;
(2)若甲取到红桃3,则乙取出的牌面数字比3大的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com