
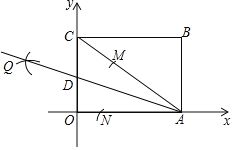
【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交AC、AO于点M、N,再分别以M、N为圆心,大于![]() MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
MN长为半径画弧两弧交于点Q,作射线AQ交y轴于点D,则点D的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
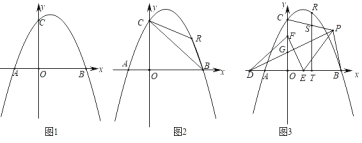
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销A、B两种商品,现有如下信息:
信息1:A、B两种商品的进货单价之和是3元;
信息2:A商品零售单价比进货单价多1元,B商品零售单价比进货单价的2倍少1元;
信息3:按零售单价购买A商品3件和B商品2件,共付12元.
请根据以上信息,解答下列问题:
(1)求A、B两种商品的零售单价;
(2)该商店平均每天卖出A商品500件和B商品1500件.经调查发现,A种商品零售单价每降0.1元,A种商品每天可多销售100件.商店决定把A商品的零售单价下降m(m>0)元,B商品的零售单价和销量都不变,在不考虑其他因素的条件下,当m为多少时,商品每天销售A、B两种商品获取的总利润为2000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
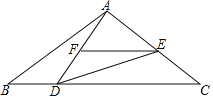
【题目】如图:已知在△ABC中,AB=AC,点D是BC上一点,∠ADE=∠B,
(1)求证:△ABD~△DCE;
(2)点F在AD上,且![]() =
=![]() ,求证:EF∥CD.
,求证:EF∥CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华星商店准备从阳光机械厂购进甲、乙两种零件进行销售,若一个甲种零件的进价比一个乙种零件的进价多50元,用4000元购进甲种零件的数量是用1500元购进乙种零件的数量的2倍.
(1)求每个甲种零件,每个乙种零件的进价分别为多少元?
(2)华星商店甲种零件每件售价为260元,乙种零件每件售价为190元,商店根据市场需求.决定向该厂购进一批零件、且购进乙种零件的数量比购进甲种零件的数量的2倍还多4个,若本次购进的两种零件全部售出后,总获利不少于2400元、求该商店本次购进甲种零件至少是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
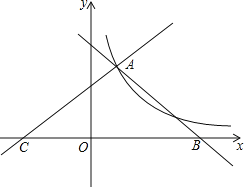
【题目】如图直线y1=-x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点
交于点A(1,m),这两条直线分别与x轴交于B,C两点
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=(a2+1)x2+bx+c经过点A(﹣3,t)、B(4,t)两点,则不等式(a2+1)(x-2)2+bx<2b-c+t的解集是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
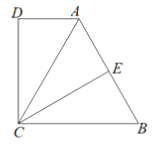
【题目】如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.
(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;
(2)当∠B=70°时,求∠AEC的度数;
(3)当△ACE为直角三角形时,求边BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com