
����Ŀ����1����ͼ1�����ı���ABCD�У���D=37������E��BC����һ�㣬��AE�۵�����B����AD��B��������B��E��CD�����B=_________����

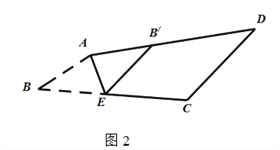
��2����ͼ2�����ı���ABCD�У�AB��CD����E��BC����һ�㣬��AE�۵�����B����AD��B��������F��BC����һ�㣬��DF�۵�����C����AD��C������B��E��C��F�к�λ�ù�ϵ��Ϊʲô��
��3����ͼ3�����ı���ABCD�У���B=��D=90������E��BC����һ�㣬��AE�۵�����B����AD��B��������F��AD����һ�㣬��CF�۵�����D����BC��D���������ʣ�AE��CF�к�λ�ù�ϵ��˵�����ɣ�

��4�����ı���ABCD�У���E��BC����һ�㣬��AE�۵���
������B�����ı���ABCD��B��������ͼ4�������1����2����BAD����B֮���������ϵΪ________��
������B�����ı���ABCD��B��������ͼ5�������1����2����BAD����B֮���������ϵΪ ______��

���𰸡���1��37����2��B��E��C��F�����ɼ��⣻��3��AE��CF�����ɼ���������4���١�1+��2=��BAD+2��B��180�����ڡ�2����1=��BAD+2��B��180��
�����������������(1)������B��E��CD�ó���AB��E=��D=37�㣬Ȼ������۵�ͼ�ε����ʵó��𰸣�(2)������AB��CD�ó���B+��C=180�㣬�����۵�ͼ�εó���AB��E=��B����DC��F=��C��Ȼ�����ƽ�ǵ����ʵó���DC��F=��EB��C���Ӷ��ó��𰸣�(3)�����ݡ�B+��D=180���ó���BAD+��DCB=180�㣬Ȼ������۵�ͼ�ε����ʵó���BAE+��FCD��=90�㣬���ݡ�B�Ķ����ó���BAE+��AEB=90�㣬�Ӷ��õ���AEB=��FCD�䣬���ó�ƽ�У�(4)������ƽ���ߵ����ʡ��۵�ͼ�ε������Լ������ε��ڽǺͶ����ó�����֮��Ĺ�ϵ��
���������(1)����B��E��CD�� ���AB��E=��D=37�㣬�����۵�ͼ�Σ����B=��AB��E=37�㣻
(2)����AB��CD�����B+��C=180�㣬�����۵�ͼ�Σ� ���AB��E=��B����DC��F=��C��
���AB��E+��DC��F=180�㣬�ߡ�AB��E+��EB��C=180�㣬���DC��F=��EB��C��
��B��E��C��F��
(3)���ߡ�B+��D=180�㣬 ���BAD+��DCB=180�㣬
�����۵�ͼ�Σ� ���BAE+��FCD��=180���2=90�㣬�ߡ�B=90�㣬
���BAE+��AEB=90�㣬���AEB=��FCD�䣬��AE��FC��
(4)���١���1+��2=��BAD+2��B��180����
�ڡ���2����1=��BAD+2��B��180����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
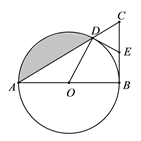
����Ŀ����ͼ����ABC�У���ABC��90������ABΪֱ������O��AB�ڵ�D����EΪBC���е㣬����OD��DE��
�� ��֤��OD��DE��
�� ����BAC��30����AB��8������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
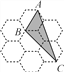
����Ŀ����ͼ����7����״����С��ȫ��ͬ������������ɵ������������εĶ����Ϊ��㣮��֪ÿ���������εı߳�Ϊ1����ABC�Ķ��㶼�ڸ���ϣ����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
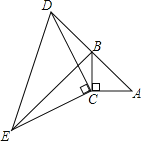
����Ŀ����ͼ������ABC�У���ACB=90����AC=BC���ӳ�AB����D��ʹDB=AB������CD����CDΪֱ�DZ�������ֱ��������CDE�����С�DCE=90��������BE.
��1����֤����ACD�ա�BCE��
��2)��AC=3����BE�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵ���![]() �͵���
�͵���![]() �У�б��
�У�б��![]() �е�
�е�![]() Ҳ��
Ҳ��![]() ���е㣬
���е㣬![]() ��
��![]() ��
��
��![]() ����ͼ����
����ͼ����![]() ��
��![]() �Ĺ�ϵ��__________��
�Ĺ�ϵ��__________��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ���뻭��ͼ�ξ���
���뻭��ͼ�ξ���![]() ��ֵ��
��ֵ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת���Ƕ�Ϊ
��ʱ����ת���Ƕ�Ϊ![]() �����жϣ�
�����жϣ�![]() ���Ľ����Ƿ���Ȼ��������������֤�������������뻭ͼ˵����
���Ľ����Ƿ���Ȼ��������������֤�������������뻭ͼ˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
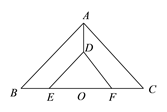
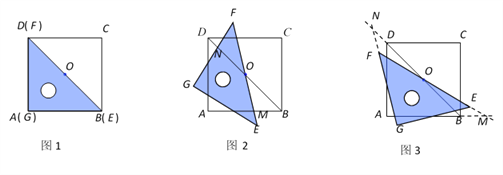
����Ŀ����ͼ1��һ����ֱ�����dz�GEF������ֱ�DZ���������ABCD�������߷ֱ��غ���һ����������ABCD���ֲ����������dz�GEF��б��EF���е�O����OҲ��BD�е㣩��˳ʱ�뷽����ת��
��1����ͼ2����EF��AB�ཻ�ڵ�M��GF��BD�ཻ�ڵ�Nʱ��ͨ���۲�����BM��FN�ij��ȣ�����BM��FN�����������ϵ����֤����IJ��룻
��2�������dz�GEF��ת����ͼ3��ʾ��λ��ʱ���߶�FE���ӳ�����AB���ӳ����ཻ�ڵ�M���߶�BD���ӳ�����GF���ӳ����ཻ�ڵ�N����ʱ����1���еIJ��뻹����������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����Rt��ABC�У���C=90�㣬��һ�ڽ�������DEFC������AF��DE��G����AC=15��BC=10��
��1����������DEFC�ı߳�����2����EG�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
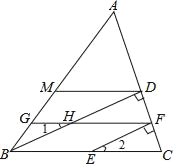
����Ŀ����ͼ��BD�AAC ��D��EF�AAC ��F����AMD=��AGF����1=��2=35��
��1�����GFC�Ķ�����
��2����֤��DM��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����������ʽ��a+b��2��ʾa��b�����͵�ƽ��������������գ�
����ʽa2��b2��ʾ_____��
����ʽ��a+b����a��b����ʾ_____��
��2���Լ���a��bȡ��ͬ��ֵʱ��a2��b2����a+b����a��b����ֲ�������±���

��3�������������a��b��ȡһ����ֵ��������a2��b2����a+b����a��b����ֲ��
��a=_____��b=_____ʱ��a2��b2=_____����a+b����a��b��=_____��
��4���ҵķ��֣�_____��
��5�����㷢�ֵĹ��ɼ��㣺78.352��21.652��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com