
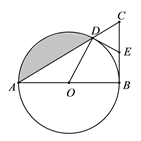
【题目】如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE.
⑴ 求证:OD⊥DE.
⑵ 若∠BAC=30°,AB=8,求阴影部分的面积.
【答案】![]()
【解析】试题分析:(1)连接BD,易得BDC是直角三角形,E是中点,所以DE=BE,∠CBD=∠EDB,通过倒角知.
(2)用扇形面积减去三角形OAD面积就是阴影部分的面积,其中∠AOD是120°.
试题解析:
⑴ 连接DB.
∵ AB是⊙O的直径 ,
∴ ∠ADB=90°,
∴ ∠CDB=90°,
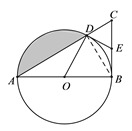
∵ 点E是BC的中点, ∴ DE=CE=![]() ,
,
∴ ∠EDC=∠C,
∵ OA=OD,∴ ∠A=∠ADO,
∵ ∠ABC=90°, ∠A+∠C=90° ,
∴ ∠ADO+∠EDC=90°,
∴ ∠ODE=90°,
∴ OD⊥DE.
⑵∵∠BAC=30°,![]() ∠AOD=120°,
∠AOD=120°,
![]()
![]() cm2,
cm2,
∵AB=8,AO=4, ![]() 勾股定理知AD=4
勾股定理知AD=4![]() ,O到AD的距离是2,
,O到AD的距离是2,
![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在同一个直角坐标系中作出y=![]() x2,y=
x2,y=![]() x2-1的图象.
x2-1的图象.
(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y=![]() x2-1与抛物线y=
x2-1与抛物线y=![]() x2有什么关系?
x2有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
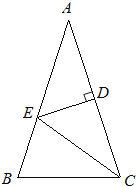
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
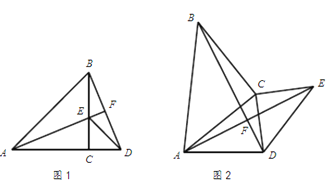
【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5,
①求证:AF⊥BD; ②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线CF,标出F点;
(2)过点B画AC的垂线BG,垂足为点G,标出G点;
(3)点B到AC的距离是线段 的长度;
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读材料,再尝试解决问题:
完全平方式![]() 以及
以及![]() 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求![]() 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
例如:①用配方法解题如下: ![]()
原式=![]() +6x+9+1=
+6x+9+1=![]()
因为无论![]() 取什么数,都有
取什么数,都有![]() 的值为非负数,所以
的值为非负数,所以![]() 的最小值为0;此时
的最小值为0;此时![]() 时,进而
时,进而![]() 的最小值是0+1=1;所以当
的最小值是0+1=1;所以当![]() 时,原多项式的最小值是1.
时,原多项式的最小值是1.
请根据上面的解题思路,探求:
(1)若(x+1)2+(y-2)2=0,则x= ,y= ..
(2)若x2+y2+6x-4y+13=0,求x,y的值;
(3)求![]() 的最小值
的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)
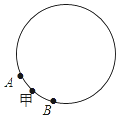
查看答案和解析>>
科目:初中数学 来源: 题型:
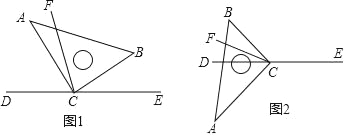
【题目】直角三角板ABC的直角顶点C在直线DE上,CF平分∠BCD.
(1)在图1中,若∠BCE=40°,求∠ACF的度数;
(2)在图1中,若∠BCE=α,直接写出∠ACF的度数(用含α的式子表示);
(3)将图1中的三角板ABC绕顶点C旋转至图2的位置,探究:写出∠ACF与∠BCE的度数之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形ABCD中,∠D=37°,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,若B′E∥CD,则∠B=_________°.

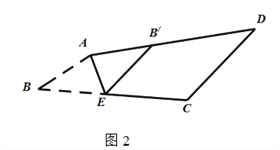
(2)如图2,在四边形ABCD中,AB∥CD,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,点F是BC边上一点,沿DF折叠,点C落在AD上C′处.B′E与C′F有何位置关系?为什么?
(3)如图3,在四边形ABCD中,∠B=∠D=90°,点E是BC边上一点,沿AE折叠,点B落在AD上B′处,点F是AD边上一点,沿CF折叠,点D落在BC上D′处.试问:AE与CF有何位置关系?说明理由.

(4)在四边形ABCD中,点E是BC边上一点,沿AE折叠.
①若点B落在四边形ABCD内B′处(如图4),则∠1,∠2,∠BAD,∠B之间的数量关系为________.
②若点B落在四边形ABCD外B′处(如图5),则∠1,∠2,∠BAD,∠B之间的数量关系为 ______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com