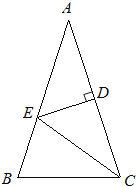
【题目】如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC．
（1）求∠ECD的度数；
（2）若CE＝5，求BC长．
【答案】（1）36°；（2）5
【解析】试题分析：
（1）ED是AC的垂直平分线，可得AE＝EC；∠A＝∠C；已知∠A＝36，即可求得；
（2）△ABC中，AB＝AC，∠A＝36°，可得∠B＝72°，又∠BEC＝∠A＋∠ECA＝72°，所以BC＝EC＝5．
试题解析：
解：（1）∵DE垂直平分AC，∠A＝36°∴CE＝AE，∴∠ECD＝∠A＝36°；（2）∵AB＝AC，∠A＝36°，∴∠B＝∠ACB＝72°，∴∠BEC＝∠A＋∠ECD＝72°，∴∠BEC＝∠B，∴BC＝EC＝5．
（2）∵AB＝AC，∠A＝36°，∴∠B＝（180°-36°）÷2=72°.
∵∠BEC＝∠A＋∠ECA＝72°，∴CE=CB，∴BC＝EC＝5．
科目：初中数学 来源： 题型：
【题目】某工厂接到一批服装加工业务，若由甲车间独做，可比规定时间提前8天完成，甲车间在制作完这批服装的60%后因另有任务，立即将剩余服装全部交给乙车间，结果刚好按规定时间完成．已知甲、乙两个车间每天分别制作200和120件服装，求该工厂所接的这批服装的件数和规定时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解学生参加户外活动的情况，和谐中学对学生每天参加户外活动的时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：
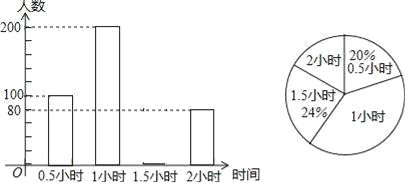
（1）求被抽样调查的学生有多少人？并补全条形统计图；
（2）该校共有1850名学生，请估计该校每天户外活动时间超过1小时的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请把下面证明过程补充完整：
已知：如图，∠ADC＝∠ABC，BE、DF分别平行∠ABC、∠ADC，且∠1＝∠2．
求证：∠A＝∠C．
证明：因为BE、DF分别平分∠ABC、∠ADC，（ ）．
所以∠1＝
∠ABC，∠3＝
∠ADC（ ）．
因为∠ABC＝∠ADC（已知），
所以∠1＝∠3（ ），
因为∠1＝∠2（已知），
所以∠2＝∠3（ ）．
所以 ∥ （ ）．
所以∠A＋∠ ＝180°，∠C＋∠ ＝180°（ ）．
所以∠A＝∠C（ ）．
查看答案和解析>>
科目：初中数学 来源： 题型：
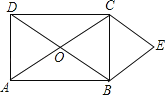
【题目】平行四边形ABCD的对角线AC和BD交于O点，分别过顶点B，C作两对角线的平行线交于点E，得平行四边形OBEC．
（1）如果四边形ABCD为矩形（如图），四边形OBEC为何种四边形？请证明你的结论；
（2）当四边形ABCD是 形时，四边形OBEC是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，E为AC上一点，且AE=BC，过点A作AD⊥CA，垂足为A，且AD=AC，AB、DE交于点F．试判断线段AB与DE的数量关系和位置关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】推理填空：
如图，已知∠1＝∠2，∠B＝∠C，可推得AB∥CD.理由如下：
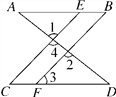
∵∠1＝∠2(已知)，且∠1＝∠4(____________)，
∴∠2＝∠4(等量代换)，
∴CE∥BF(__________________________)，
∴∠________＝∠3(______________________)．
又∵∠B＝∠C(已知)，
∴∠3＝∠B(等量代换)．
∴AB∥CD(__________________________)．
查看答案和解析>>
科目：初中数学 来源： 题型：
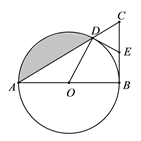
【题目】如图，△ABC中，∠ABC＝90°，以AB为直径的⊙O交AB于点D，点E为BC的中点，连接OD、DE．
⑴ 求证：OD⊥DE．
⑵ 若∠BAC＝30°，AB＝8，求阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
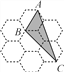
【题目】如图是由7个形状、大小完全相同的正六边形组成的网格，正六边形的顶点称为格点．已知每个正六边形的边长为1，△ABC的顶点都在格点上，求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com