
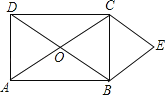
【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是 形时,四边形OBEC是正方形.
【答案】(1)证明见解析;(2)正方
【解析】(1)根据矩形的性质:两条对角线相等且互相平分,即可得到结论;(2)根据正方形的性质:对角线相等且互相垂直平分,即可得到结论.
解:(1)四边形OBEC是菱形.理由如下:
∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是矩形,
∴OC=![]() AC; OB=
AC; OB=![]() BD;AC=BD
BD;AC=BD
∴OC=OB,
∴平行四边形OBEC为菱形;
(2) 四边形ABCD是正方形时,四边形OBEC是正方形. 理由如下:
四边形OBEC是菱形.
∵BE∥OC,CE∥OB,
∴四边形OBEC为平行四边形.
又∵四边形ABCD是正方形,
∴OC=![]() AC; OB=
AC; OB=![]() BD;AC=BD且AC⊥BD
BD;AC=BD且AC⊥BD
∴OC=OB,∠BOC=90,
∴平行四边形OBEC为正方形;
即:当四边形ABCD是正方形时,四边形OBEC是正方形.


科目:初中数学 来源: 题型:
【题目】如图所示,正五边形ABCDE的对角线AC、BE相交于M.
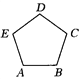
(1)求证:四边形CDEM是菱形;
(2)设MF2=BE·BM,若AB=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(1+a)(1-a)+(a-2)2,其中a=![]() ;
;
(2)(2x+3)(2x-3)-4x(x-1)+(x-2)2,其中x=-3.
查看答案和解析>>
科目:初中数学 来源: 题型:
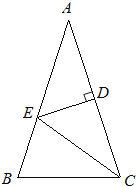
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人两次同时在同一家粮店购买粮食(假设两次购买粮食的单价不相同),甲每次购买
粮食100千克,乙每次购买粮食用去100元.
(1)假设![]() 、
、![]() 分别表示两次购买粮食时的单价(单位:元/千克),试用含
分别表示两次购买粮食时的单价(单位:元/千克),试用含![]() 、
、![]() 的代数式表示:甲两次购
的代数式表示:甲两次购
买粮食共需付款 元,乙两次共购买 千克粮食;若甲两次购买粮食的平均单价为每千
克![]() 元,乙两次购买粮食的平均单价为每千克
元,乙两次购买粮食的平均单价为每千克![]() 元,则
元,则![]() = ,
= ,![]() = .
= .
(2)若谁两次购买粮食的平均单价低,谁购买粮食的方式就较合算.请你判断甲、乙两人购买粮食的方式哪一个较合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线CF,标出F点;
(2)过点B画AC的垂线BG,垂足为点G,标出G点;
(3)点B到AC的距离是线段 的长度;
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,平行四边形
,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .将直线
.将直线![]() 绕点
绕点![]() 顺时针旋转分别交
顺时针旋转分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(![]() )在旋转过程中,线段
)在旋转过程中,线段![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(![]() )如图
)如图![]() ,若
,若![]() ,当旋转角至少为__________
,当旋转角至少为__________![]() 时,四边形
时,四边形![]() 是平行四边形,并证明此时的四边形是
是平行四边形,并证明此时的四边形是![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com