
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价).这两种服装的进价,标价如表所示.
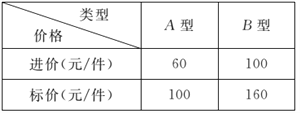
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
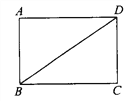
【题目】(1)如图,小林同学想把一张矩形的纸沿对角线BD对折,对折后C点与C′点重合,BC和AD相交于E,请你用尺规作图的方法作出C′点,并保留作图痕迹.
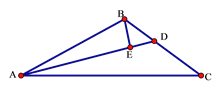
(2)如图,已知在△ABC中,∠ABC=3∠C,AD是∠BAC的平分线,BE⊥AD于E,求证:BE=![]() (AC-AB)
(AC-AB)
查看答案和解析>>
科目:初中数学 来源: 题型:
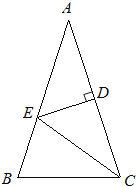
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
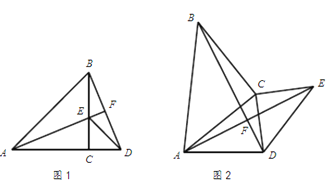
【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5,
①求证:AF⊥BD; ②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读材料,再尝试解决问题:
完全平方式![]() 以及
以及![]() 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求![]() 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
例如:①用配方法解题如下: ![]()
原式=![]() +6x+9+1=
+6x+9+1=![]()
因为无论![]() 取什么数,都有
取什么数,都有![]() 的值为非负数,所以
的值为非负数,所以![]() 的最小值为0;此时
的最小值为0;此时![]() 时,进而
时,进而![]() 的最小值是0+1=1;所以当
的最小值是0+1=1;所以当![]() 时,原多项式的最小值是1.
时,原多项式的最小值是1.
请根据上面的解题思路,探求:
(1)若(x+1)2+(y-2)2=0,则x= ,y= ..
(2)若x2+y2+6x-4y+13=0,求x,y的值;
(3)求![]() 的最小值
的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织初一同学春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座大客车,则多出一辆,且其余客车恰好坐满.已知45座客车日租金为每辆220元,60座大客车日租金为每辆300元.
求:(1)初一年级学生有多少人? 原计划租用45座客车多少辆?
(2)要使每个学生都有座位,怎样租用更合算?最低租金是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com