
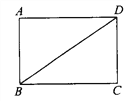
【题目】(1)如图,小林同学想把一张矩形的纸沿对角线BD对折,对折后C点与C′点重合,BC和AD相交于E,请你用尺规作图的方法作出C′点,并保留作图痕迹.
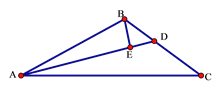
(2)如图,已知在△ABC中,∠ABC=3∠C,AD是∠BAC的平分线,BE⊥AD于E,求证:BE=![]() (AC-AB)
(AC-AB)
【答案】(1)作图见解析;(2)证明见解析
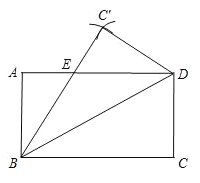
【解析】试题分析:(1)分别以B、D为圆心,以BC、CD的长为半径画弧,两弧的交点就是所要找的点C′;
(2)根据全等三角形的判定与性质,可得∠ABF=∠AFB,AB=AF,BE=EF,根据三角形外角的性质,可得∠C+∠CBF=∠AFB=∠ABF,根据角的和差、等量代换,可得∠CBF=∠C,根据等腰三角形的判定,可得BF=CF,根据线段的和差、等式的性质,可得答案.
试题解析:
(1)分别以B为圆心,以BC为半径画弧,以D为圆心,以DC为半径画弧,两弧在AD的上方相交于一点C′,
则C′为所要画的点. 保留作图痕迹。
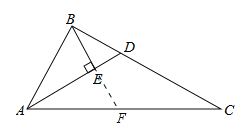
(2)证明:延长BE交AC于F,如图所示:
∵AD是∠BAC的平分线,
∴∠BAE=∠FAE.
在△BAE和△FAE中,
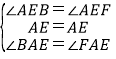
∴△BAE≌△FAE,
∴∠ABF=∠AFB,BE=FE,AB=AF,
∴BE=![]() BF,
BF,
∠ABC=∠ABF+∠FBC=∠AFB+∠FBC=(∠C+∠FBC)+∠FBC=∠C+2∠FBC,
又∵∠ABC=3∠C,
∴3∠C=∠C+2∠FBC,
∴∠FBC=∠C,
∴BF=CF,
∴BE=![]() CF,
CF,
∵CF=AC-AF=AC-AB,
∴BE=![]() CF=
CF=![]() (AC-AB).
(AC-AB).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AD=BC,AC,BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H.
(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线)
(2)证明:四边形AHBG是菱形;
(3)若使四边形AHBG是正方形,还需在Rt△ABC的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与AC相切于点A,且AB=AC,BC与⊙O相交于点D,下列说法不正确的是().
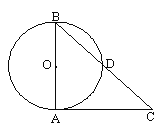
A. ∠C = 45° B. CD=BD C. ∠BAD=∠DAC D. CD=AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
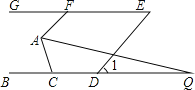
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整:
已知:如图,∠ADC=∠ABC,BE、DF分别平行∠ABC、∠ADC,且∠1=∠2.
求证:∠A=∠C.
证明:因为BE、DF分别平分∠ABC、∠ADC,( ).
所以∠1=![]() ∠ABC,∠3=
∠ABC,∠3=![]() ∠ADC( ).
∠ADC( ).
因为∠ABC=∠ADC(已知),
所以∠1=∠3( ),
因为∠1=∠2(已知),
所以∠2=∠3( ).
所以 ∥ ( ).
所以∠A+∠ =180°,∠C+∠ =180°( ).
所以∠A=∠C( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
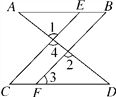
∵∠1=∠2(已知),且∠1=∠4(____________),
∴∠2=∠4(等量代换),
∴CE∥BF(__________________________),
∴∠________=∠3(______________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(__________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.

(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com