
【题目】把一张对边互相平行的纸条,折成如图所示,![]() 是折痕,若
是折痕,若![]() ,则下列结论正确的有( )
,则下列结论正确的有( )

(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:根据平行线的性质和折叠的性质判断.
详解:(1)因为AC′∥BD′,所以∠C′EF=∠EFB,
因为∠EFB=32°,所以∠C′EF=32°,则(1)正确;
(2)根据折叠的性质,∠CEC′=2∠C′EF=2×32°=64°,
所以∠AEC=180°-∠CEC′=180°-64°=116°,则(2)错误;
(3)因为AC′∥BD′,所以∠C′EC=∠AEG,
所以∠AEG=64°,则(3)正确;
(4)根据折叠的性质得,∠EFD=∠EFD′,
因为AC′∥BD′,所以∠C′EF+∠EFD′=180°,
所以∠EFD′=180°-32°=148°.
所以∠BFD=∠EFD-∠EFB=148°-32°=116°,则(4)正确.
故选C.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+c与抛物线y=ax2+bx+c的图像都经过y轴上的D点,抛物线与x轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的是( ) ①abc>0; ②3a+b>0; ③﹣1<k<0; ④4a+2b+c<0; ⑤a+b<k.
A.①②③
B.②③⑤
C.②④⑤
D.②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
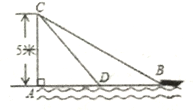
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=6,BC=8,tan∠B= ![]() ,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )
,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线OA是某正比例函数的图象,下列各点在该函数图象上的是( )
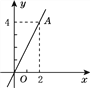
A. (-4,16) B. (3,6) C. (-1,-1) D. (4,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, ![]() ABC的三个顶点坐标分别为A(3,5),B(4,3),
ABC的三个顶点坐标分别为A(3,5),B(4,3),
C(1,1).
(1)画出![]() ABC关于x轴对称的
ABC关于x轴对称的![]() A1B1C1;并填写出
A1B1C1;并填写出![]() A1B1C三个顶点的坐标.
A1B1C三个顶点的坐标.
A1 (_________,_________);
B1 (_________,________);
C1 (_________,_________).
(2)求![]() ABC的面积.
ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠l=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.

解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90° ( )
∴∠DEB+( )=180°
∴DE∥AB ( )
∴∠1=∠A( )
∠2=∠3( )
∵∠l=∠2(已知)
∴∠A=∠3( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直径坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C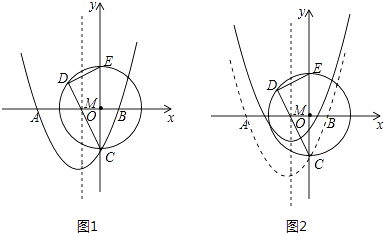
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移 ![]() 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() 为直线
为直线![]() 上一点,
上一点, ![]() 为直线
为直线![]() 上一点,
上一点, ![]() ,设
,设![]() ,
, ![]() .
.
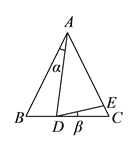
(![]() )如图,若点
)如图,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上.
上.
①如果![]() ,
, ![]() ,那么
,那么![]() __________,
__________, ![]() __________.
__________.
②求![]() ,
, ![]() 之间的关系式.
之间的关系式.
(![]() )是否存在不同于以上②中的
)是否存在不同于以上②中的![]() ,
, ![]() 之间的关系式?若存在,求出这个关系式,(求出一种不同于②中的关系即可),若不存在,请说明理由.
之间的关系式?若存在,求出这个关系式,(求出一种不同于②中的关系即可),若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com