Question

【题目】如图,在四边形中,于点,于点,平分,且点为的中点,连接.

(1)求证：平分；

(2)求的度数．

Answer 1

【答案】（1）见解析；（2）∠AED=90°.

【解析】

（1）过点E作EF⊥AD于F，根据角平分线上的点到角的两边距离相等可得CE=EF，再求出BE=EF，然后根据到角的两边距离相等的点在角的平分线上证明；
（2）求出DC∥AB，求出∠CDA+∠BAD=180°，根据角平分线定义得出∠EAD=∠BAD，∠EDA=∠CDA，求出∠EAD+∠EDA=90°，即可求出答案．

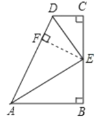
(1)证明：如图,过点E作EF⊥AD于F,

∵∠C=90°，DE平分∠ADC，
∴CE=EF，
∵E是BC的中点，
∴BE=CE，
∴BE=EF，
又∵∠B=90°，EF⊥AD，
∴AE平分∠BAD；
(2)∵∠C=∠B=90°，
∴∠D+∠B=180°，
∴DC∥AB，
∴∠CDA+∠BAD=180°，
∵DE平分∠ADC，AE平分∠BAD，
∴∠EAD=∠BAD,∠EDA=∠CDA，
∴∠EAD+∠EDA=90°，
∴∠AED=180°90°=90°.