
【题目】如图,计划围一个面积为50 m2的长方形场地,一边靠旧墙(墙长为10 m),另外三边用篱笆围成,并且它的长与宽之比为5∶2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
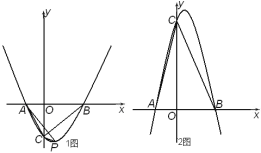
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴分别交于点A、B(A左B右),与
轴分别交于点A、B(A左B右),与![]() 轴交于点C,顶点是P.
轴交于点C,顶点是P.
(1)则A点坐标是:________;B点坐标是:________;
(2)当![]() 时,如1图所示:设△ACP的面积为
时,如1图所示:设△ACP的面积为![]() ,△ABC的面积为
,△ABC的面积为![]() ,求
,求![]() 的值;
的值;
(3)当![]() 且∠ACB=45°时,如2图所示:求此二次函数的解析式.
且∠ACB=45°时,如2图所示:求此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
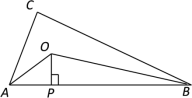
【题目】如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,BC=12.点O为∠ABC与∠CAB的平分线的交点,则点O到边AB的距离OP为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD的外侧,作△ADE和△DCF,连接AF、BE.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠ABC=∠BCD=∠CDA=∠DAB=90°)
(1)如图①,若△ADE和△DCF是等边三角形,求证:AF=BE,AF⊥BE;
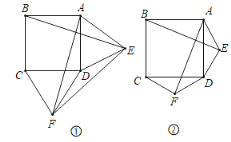
(2)如图②,若△ADE和△DCF为一般三角形,其中AE=DF,ED=FC,则第(1)问中的结论仍然成立吗?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在的联系,它是“数形结合”的基础,请利用数轴解决下列问题:
(1)画出数轴,并在数轴上画出表示下列各数的点:![]()
(2)用“>”号将(1)中各数连接起来;
(3)直接填空:数轴上若![]() 点表示的数为
点表示的数为![]() 点表示的数为-2,则
点表示的数为-2,则![]() 之间的距离是 .
之间的距离是 .
(4)直接填空:若数轴上![]() 点表示的数为
点表示的数为![]() ,且
,且![]() 两点间的距离为
两点间的距离为![]() ,则
,则![]() 点表示的数为 .
点表示的数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信(一种聊天软件)的兴起,许多人抓住这种机会,做起了“微商”很多农产品也改变了原来的销售模式,实行了网上销售,刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖![]() 斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负单位:斤);
斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负单位:斤);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 斤;
(2)根据记录的数据可知该周销售量最多的一天比销售量最少的一天多销售 斤;
(3)本周实际销售总量是否达到了计划数量?试通过计算说明理由.
(4)若冬枣每斤按![]() 元出售,每斤冬枣的运费平均
元出售,每斤冬枣的运费平均![]() 元(运费由小明承担),那么小明本周一共收入多少元?
元(运费由小明承担),那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由若干个完全相同的小正方体组成的几何体.
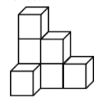

(1)请画出这个几何体从不同方向看到的图形
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体从正面看和从上面看形状不变,那么最多可以再添加多少个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
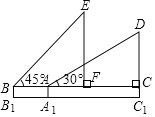
【题目】如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米.
(1)当风筝的水平距离AC=18米时,求此时风筝线AD的长度;
(2)当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com