
【题目】在正方形ABCD的外侧,作△ADE和△DCF,连接AF、BE.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠ABC=∠BCD=∠CDA=∠DAB=90°)
(1)如图①,若△ADE和△DCF是等边三角形,求证:AF=BE,AF⊥BE;
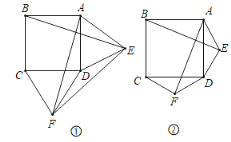
(2)如图②,若△ADE和△DCF为一般三角形,其中AE=DF,ED=FC,则第(1)问中的结论仍然成立吗?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)证明见详解;(2)成立,证明见详解
【解析】
(1)根据正方形的性质、等边三角形的性质以及全等三角形的判定定理证明△BAE≌△ADF,根据全等三角形的性质得出结论;
(2)根据边边边定理证明△EAD≌△FDC.根据边角边定理证明△BAE≌△ADF.则BE=AF,∠ABE=∠DAF,与(1)的证明方法相似,可得结论.
解:(1)AF=BE;AF⊥BE.
理由如下:如图①所示:
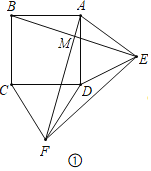
∵四边形ABCD是正方形,
∴∠BAD=∠ADC=90°,AB=AD=CD,
∵△ADE和△DCF是等边三角形,
∴∠DAE=∠CDF=60°,AE=AD,DF=CD,
∴AE=DF,∠BAE=∠ADF=150°,
在△BAE和△ADF中,
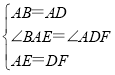
∴△BAE≌△ADF(SAS),
∴AF=BE,∠ABE=∠DAF,
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴∠AMB=90°,
∴AF⊥BE;
故答案为:AF=BE,AF⊥BE.
(2)所画图形如图②,第(1)问的结论成立,理由如下:
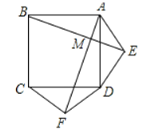
②
在△AED和△DFC中,
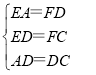
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.即∠BAE=∠ADF.
在△BAE和△ADF中,
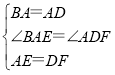
∴△BAE≌△ADF(SAS),
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴∠AMB=90°,
∴AF⊥BE.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(﹣5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批A、B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等.
(1)求该公司购买的A、B型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条A型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,计划围一个面积为50 m2的长方形场地,一边靠旧墙(墙长为10 m),另外三边用篱笆围成,并且它的长与宽之比为5∶2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
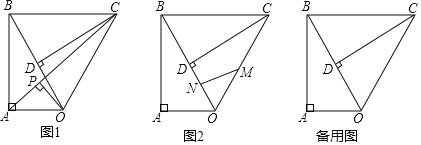
【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如题图1,连接BC.
(1)填空:∠OBC= °;
(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;
(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为89.6%,把实验数据绘制成图1和图2所示的两幅不完整的统计图.
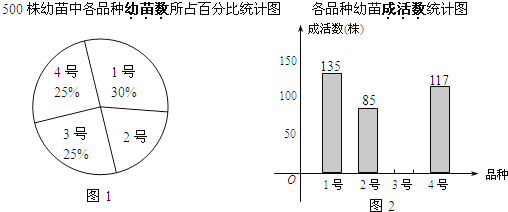
(1)实验所用的2号茶树幼苗的数量是 株;
(2)求出3号茶树幼苗的成活数,并补全统计图2;
(3)该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出1号品种被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com