练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

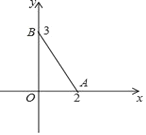
    【题目】在平面直角坐标系中，有点A(2，0)，B(0，3)，C(0，2)，且△AOB与△OCD全等．请直接写出点D的坐标________.

    【答案】（3，0），（－3，0），（3，2）或（－3，2）

    【解析】

    分情况讨论：①当OB=OD=3时，②当OB=CD=3时，分别作出图形，求出对应的点D的坐标即可.

    解：①当OB=OD=3时，如图△COD1≌△AOB，△COD4≌△AOB，此时D点坐标为：（3，0），（－3，0）；

    ②当OB=CD=3时，如图，△OCD2≌△AOB，△OCD3≌△AOB，此时D点坐标为：（3，2），（－3，2）；

    综上所述，△AOB与△OCD全等时，点D的坐标为：（3，0），（－3，0），（3，2）或（－3，2）；

    故答案为：（3，0），（－3，0），（3，2）或（－3，2）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在∠△ACB和△DCE中，AC＝BC，CD＝CE，∠ACB＝∠DCE＝90°，连接AE、BD交于点O，AE与DC交于点M，BD与AC交于点N．

    (1)试判断AE、BD之间的关系，并说明理由；

    (2)连接CO，则下面两个结论中选择你认为正确的一个加以说明①射线CO平分∠ACD ②射线OC平分∠BOE

    查看答案和解析>>

    科目：初中数学 来源： 题型：

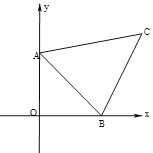
    【题目】如图，在平面直角坐标系中，A(0，3)，B(3，0)，C(5，4)，∠OAB=∠OBA=45°，点P为坐标系中第一象限内一点(不与C重合)，若△BAP≌△ABC，则点P坐标为_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB延长线于点F，则EF的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】本学期，大兴区开展了“恰同学少年，品诗词美韵”中华传统诗词大赛活动小江统计了班级30名同学四月份的诗词背诵数量，具体数据如表所示：

    诗词数量首

    4

    5

    6

    7

    8

    9

    10

    11

    人数

    3

    4

    4

    5

    7

    5

    1

    1

    那么这30名同学四月份诗词背诵数量的众数和中位数分别是　　

    A. 11，7 B. 7，5 C. 8，8 D. 8，7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠AOB.求作：∠AOB的平分线.(要求：尺规作图，保留作图痕迹，不必写作法)，这种尺规作图得到角平分线的依据是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】操作体验

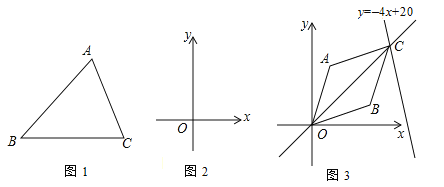
    （1）如图1，已知△ABC，请画出△ABC的中线AD，并判断△ABD与△ACD的面积大小关系．

    （2）如图2，在平面直角坐标系中，△ABC的边BC在x轴上，已知点A（2，4），B（–1，0），C（3，0），试确定过点A的一条直线l，平分△ABC的面积，请写出直线l的表达式．

    综合运用

    （3）如图3，在平面直角坐标系中，如果A（1，4），B（3，2），那么在直线y=–4x+20上是否存在一点C，使直线OC恰好平分四边形OACB的面积？若存在，请计算点C的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图书馆与学校相距600m，明明从学校出发步行去图书馆，亮亮从图书馆骑车去学校两人同时出发，匀速相向而行，他们与学校的距离S（m）与时间t（s）的图象如图所示：

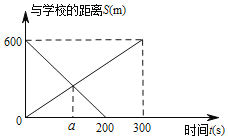
    根据图象回答：

    （1）明明步行的速度为　 　m/s；亮亮骑车的速度为　 　m/s．

    （2）分別写出明明、亮亮与学校的距离S1、S2与时间t的关系式．

    （3）通过计算求出a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD的外侧，作△ADE和△DCF，连接AF、BE．(友情提醒：正方形的四条边都相等，即AB＝BC＝CD＝DA；四个内角都是90°，即∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°)

    （1）如图①，若△ADE和△DCF是等边三角形，求证：AF＝BE，AF⊥BE；

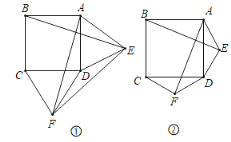
    （2）如图②，若△ADE和△DCF为一般三角形，其中AE＝DF，ED＝FC，则第（1）问中的结论仍然成立吗?若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    同步练习册答案