
【题目】某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为89.6%,把实验数据绘制成图1和图2所示的两幅不完整的统计图.
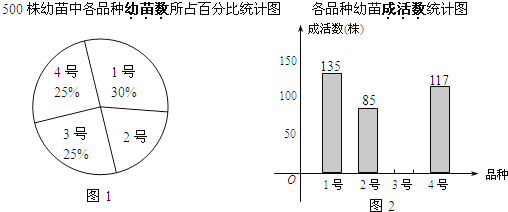
(1)实验所用的2号茶树幼苗的数量是 株;
(2)求出3号茶树幼苗的成活数,并补全统计图2;
(3)该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出1号品种被选中的概率.
【答案】(1)100;(2)3号茶树幼苗的成活数为112株,补图见解析;(3)1号品种被选中的概率为![]() .
.
【解析】(1)先根据百分比之和为1求得2号的百分比,再用总株数乘以所得百分比可得;
(2)先用总株数乘以2号的百分比求得其数量,再用2号幼苗株数乘以其成活率即可得;
(3)画树状图列出所有等可能结果,再从中找到1号品种被选中的结果数,利用概率公式计算可得.
(1)∵2号幼苗所占百分比为1﹣(30%+25%+25%)=20%,
∴实验所用的2号茶树幼苗的数量是500×20%=100株,
故答案为:100;
(2)实验所用的2号茶树幼苗的数量是500×25%=125株,
∴3号茶树幼苗的成活数为125×89.6%=112株,
补全条形图如下:
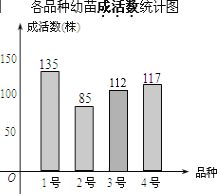
(3)画树状图如下:
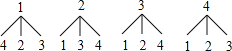
由树状图知共有12种等可能结果,其中抽到1号品种的有6种结果,
所以1号品种被选中的概率为![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD的外侧,作△ADE和△DCF,连接AF、BE.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠ABC=∠BCD=∠CDA=∠DAB=90°)
(1)如图①,若△ADE和△DCF是等边三角形,求证:AF=BE,AF⊥BE;
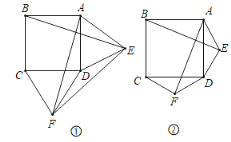
(2)如图②,若△ADE和△DCF为一般三角形,其中AE=DF,ED=FC,则第(1)问中的结论仍然成立吗?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.
(1)当点E在线段BD上移动时,如图(1)所示,求证:BC﹣DE=![]() DF.
DF.
(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段BC、DE与DF又有怎样的数量关系?请直接写出你的猜想,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某客运站行车时刻表如图,若全程保持匀速行驶,则当快车出发______小时后,两车相距25km.
哈尔滨—长春 | 出发时间 | 到站时间 | 里程(km) |
普通车 | 7:00 | 11:00 | 300 |
快车 | 7:30 | 10:30 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
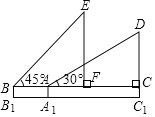
【题目】如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米.
(1)当风筝的水平距离AC=18米时,求此时风筝线AD的长度;
(2)当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
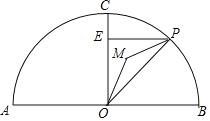
【题目】如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.
(1)求∠OMP的度数;
(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com