
【题目】如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.
(1)当点E在线段BD上移动时,如图(1)所示,求证:BC﹣DE=![]() DF.
DF.
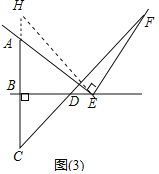
(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段BC、DE与DF又有怎样的数量关系?请直接写出你的猜想,不需证明.

【答案】(1)证明见解析;(2)如图2:DE﹣BC=![]() DF;图3:BC+DE=
DF;图3:BC+DE=![]() DF.
DF.
【解析】(1)如图1中,在BA上截取BH,使得BH=BE.构造全等三角形即可解决问题;
(2)如图2中,在BC上截取BH=BE,同法可证:DF=EH.可得:DE﹣BC=![]() DF.如图3中,在BA上截取BH,使得BH=BE.同法可证:DF=HE,可得BC+DE=
DF.如图3中,在BA上截取BH,使得BH=BE.同法可证:DF=HE,可得BC+DE=![]() DF.
DF.
(1)如图1中,在BA上截取BH,使得BH=BE.
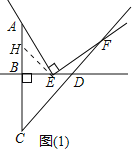
∵BC=AB=BD,BE=BH,
∴AH=ED,
∵∠AEF=∠ABE=90°,
∴∠AEB+∠FED=90°,∠AEB+∠BAE=90°,
∴∠FED=∠HAE,
∵∠BHE=∠CDB=45°,
∴∠AHE=∠EDF=135°,
∴△AHE≌△EDF,
∴HE=DF,
∴BC﹣DE=BD﹣DE=BE=![]() EH=
EH=![]() DF.
DF.
∴BC﹣DE=![]() DF.
DF.
(2)如图2中,在BC上截取BH=BE,同法可证:DF=EH.
可得:DE﹣BC=![]() DF;
DF;
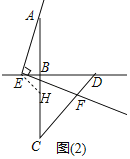
如图3中,在BA上截取BH,使得BH=BE.同法可证:DF=HE,
可得BC+DE=![]() DF.
DF.


科目:初中数学 来源: 题型:
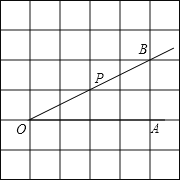
【题目】如图,点P是∠AOB的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C;
(2)过点P画OA的垂线,垂足为H;
(3)线段PH的长度是点P到______的距离,______是点C到直线OB的距离,线段PC、PH、OC这三条线段大小关系是______(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于点F,BF=AC, ∠ABE=22°,则∠CAD的度数是________°.
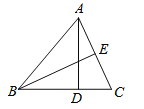
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为89.6%,把实验数据绘制成图1和图2所示的两幅不完整的统计图.
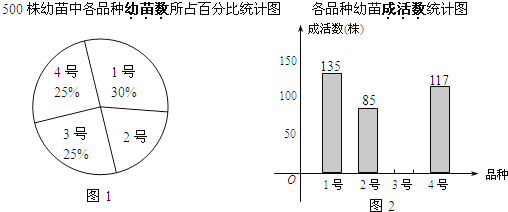
(1)实验所用的2号茶树幼苗的数量是 株;
(2)求出3号茶树幼苗的成活数,并补全统计图2;
(3)该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出1号品种被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
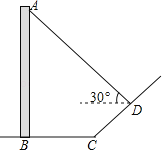
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com