
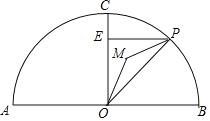
【题目】如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.
(1)求∠OMP的度数;
(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
【答案】(1)∠PMO=135°;(2)内心M所经过的路径长为2![]() πcm.
πcm.
【解析】
(1)先判断出∠MOP=∠MOC,∠MPO=∠MPE,再用三角形的内角和定理即可得出结论;
(2)分两种情况,当点M在扇形BOC和扇形AOC内,先求出∠CMO=135°,进而判断出点M的轨迹,再求出∠OO'C=90°,最后用弧长公式即可得出结论.
(1)∵△OPE的内心为M,
∴∠MOP=∠MOC,∠MPO=∠MPE,
∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣![]() (∠EOP+∠OPE),
(∠EOP+∠OPE),
∵PE⊥OC,即∠PEO=90°,
∴∠PMO=180°﹣![]() (∠EOP+∠OPE)=180°﹣
(∠EOP+∠OPE)=180°﹣![]() (180°﹣90°)=135°;
(180°﹣90°)=135°;
(2)如图,∵OP=OC,OM=OM,
而∠MOP=∠MOC,
∴△OPM≌△OCM,
∴∠CMO=∠PMO=135°,
所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(![]() 和
和![]() );
);
点M在扇形BOC内时,
过C、M、O三点作⊙O′,连O′C,O′O,
在优弧CO取点D,连DA,DO,
∵∠CMO=135°,
∴∠CDO=180°﹣135°=45°,
∴∠CO′O=90°,而OA=4cm,
∴O′O=![]() OC=
OC=![]() ×4=2
×4=2![]() ,
,
∴弧OMC的长=![]() =
=![]() π(cm),
π(cm),
同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为![]() πcm,
πcm,
所以内心M所经过的路径长为2×![]() π=2
π=2![]() πcm.
πcm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号茶树幼苗成活率为89.6%,把实验数据绘制成图1和图2所示的两幅不完整的统计图.
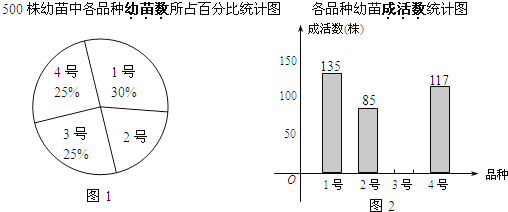
(1)实验所用的2号茶树幼苗的数量是 株;
(2)求出3号茶树幼苗的成活数,并补全统计图2;
(3)该茶农要从这四种茶树中选择两个品种进行推广,请用列表或画树状图的方法求出1号品种被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() .
.
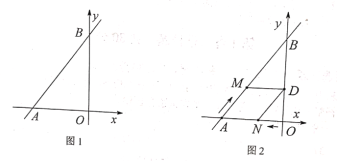
(1)直接写出直线![]() 的解析式;
的解析式;
(2)如图1,过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)如图2,点![]() 从
从![]() 出发以每秒1个单位的速度沿
出发以每秒1个单位的速度沿![]() 方向运动,同时点
方向运动,同时点![]() 从
从![]() 出发以每秒0.6个单位的速度沿
出发以每秒0.6个单位的速度沿![]() 方向运动,运动时间为
方向运动,运动时间为![]() 秒(
秒(![]() ),过点
),过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,是否存在满足条件的
,是否存在满足条件的![]() ,使四边形
,使四边形![]() 为菱形,判断并说明理由.
为菱形,判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )

A. (1)(2)(3)(4) B. (2)(4)(5) C. (2)(3)(4) D. (1)(4)(5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1 的正方体搭成的立体图形,第(1)个图形由1个正方体搭成,第(2)个图形由4个正方体搭成,第(3)个图形由10个正方体搭成,以此类推,搭成第(6)个图形所需要的正方体个数是( )
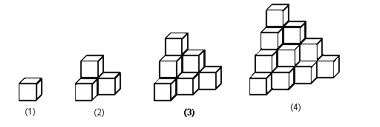
A.84个B.56个C.37个D.36个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
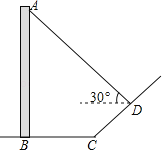
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于E,CF⊥BD于E,图中全等三角形有( )
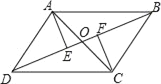
A. 3对 B. 5对 C. 6对 D. 7对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com