
【题目】在平面直角坐标系中,点![]() .
.
(1)直接写出直线![]() 的解析式;
的解析式;
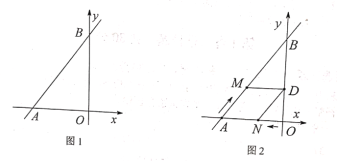
(2)如图1,过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)如图2,点![]() 从
从![]() 出发以每秒1个单位的速度沿
出发以每秒1个单位的速度沿![]() 方向运动,同时点
方向运动,同时点![]() 从
从![]() 出发以每秒0.6个单位的速度沿
出发以每秒0.6个单位的速度沿![]() 方向运动,运动时间为
方向运动,运动时间为![]() 秒(
秒(![]() ),过点
),过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,是否存在满足条件的
,是否存在满足条件的![]() ,使四边形
,使四边形![]() 为菱形,判断并说明理由.
为菱形,判断并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)利用待定系数法可求直线AB解析式;
(2)分两种情况讨论,利用全等三角形的性质可求解;
(3)先求点D坐标,由勾股定理可得DN=AM=t,可证四边形AMDN是平行四边形,即当AM=AN时,四边形AMDN为菱形,列式可求t的值.
(1)设直线AB解析式为:y=mx+n,
根据题意可得:![]() ,
,
∴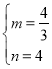 ,
,
∴直线AB解析式为![]() ;
;
(2)若点C在直线AB右侧,
如图1,过点A作AD⊥AB,交BC的延长线于点D,过点D作DE⊥AC于E,
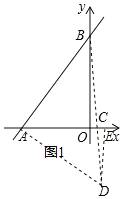
∵∠ABC=45°,AD⊥AB,
∴∠ADB=∠ABC=45°,
∴AD=AB,
∵∠BAO+∠DAC=90°,且∠BAO+∠ABO=90°,
∴∠ABO=∠DAC,AB=AD,∠AOB=∠AED=90,
∴△ABO≌△DAE(AAS),
∴AO=DE=3,BO=AE=4,
∴OE=1,
∴点D(1,-3),
∵直线y=kx+b过点D(1,-3),B(0,4).
∴![]() ,
,
∴k=-7,
若点C在点A右侧时,如图2,
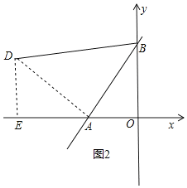
同理可得![]() ,
,
综上所述:k=-7或![]() .
.
(3)设直线DN的解析式为:y=![]() x+n,且过点N(-0.6t,0),
x+n,且过点N(-0.6t,0),
∴0=-0.8t+n,
∴n=0.8t,
∴点D坐标(0,0.8t),且过点N(-0.6t,0),
∴OD=0.8t,ON=0.6t,
∴DN=![]() =1,
=1,
∴DN=AM=1,且DN∥AM,
∴四边形AMDN为平行四边形,
当AN=AM时,四边形AMDN为菱形,
∵AN=AM,
∴t=3-0.6t,
∴t=![]() ,
,
∴当t=![]() 时,四边形AMDN为菱形.
时,四边形AMDN为菱形.


科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某客运站行车时刻表如图,若全程保持匀速行驶,则当快车出发______小时后,两车相距25km.
哈尔滨—长春 | 出发时间 | 到站时间 | 里程(km) |
普通车 | 7:00 | 11:00 | 300 |
快车 | 7:30 | 10:30 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
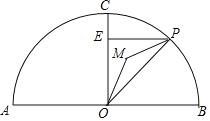
【题目】如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.
(1)求∠OMP的度数;
(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
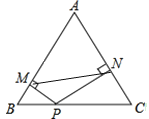
【题目】如图所示,点P是等边△ABC的BC边上一点,PM⊥AB,PN⊥AC,试猜想△AMN的周长L△AMN与四边形BMNC的周长L四边形BMNC有什么关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)在这次调查中,一共调查了 名市民.
(2)扇形统计图中,C组对应的扇形圆心角是 .
(3)请补全条形统计图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE= ![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
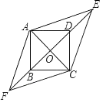
A. DE=1 B. tan∠AFO= ![]() C. AF=
C. AF= ![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com