
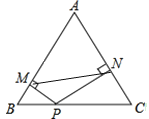
【题目】如图所示,点P是等边△ABC的BC边上一点,PM⊥AB,PN⊥AC,试猜想△AMN的周长L△AMN与四边形BMNC的周长L四边形BMNC有什么关系,并说明理由.
【答案】△AMN的周长与四边形BMNC的周长相等,理由见解析.
【解析】
依据∠BPM=∠CPN=30°,即可得出BM=![]() BP,CN=
BP,CN=![]() CP,进而求得L△AMN=AM+AN+MN=
CP,进而求得L△AMN=AM+AN+MN=![]() BC+MN;L四边形BMNC=BM+CN+BC+MN=
BC+MN;L四边形BMNC=BM+CN+BC+MN=![]() BC+MN;+
BC+MN;+
即可得到△AMN的周长与四边形BMNC的周长相等.
解:△AMN的周长与四边形BMNC的周长相等.
∵△ABC为等边三角形,
∴AB=AC=BC,∠A=∠B=∠C=60°,
又∵PM⊥AB,PN⊥AC,
∴∠BMP=∠CNP=90°,
∴∠BPM=∠CPN=30°,
∴BM=![]() BP,CN=
BP,CN=![]() CP,
CP,
∴L△AMN=AM+AN+MN
=(AB﹣BM)+(AC﹣CN)+MN
=(AB+AC)﹣(BM+CN)+MN
=2BC﹣![]() (PB+PC)+MN
(PB+PC)+MN
=2BC﹣BC+MN
=![]() BC+MN;
BC+MN;
L四边形BMNC=BM+CN+BC+MN
=![]() (PB+PC)+BC+MN
(PB+PC)+BC+MN
=![]() BC+BC+MN
BC+BC+MN
=![]() BC+MN;
BC+MN;
∴L△AMN=L四边形BMNC.


科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() .
.
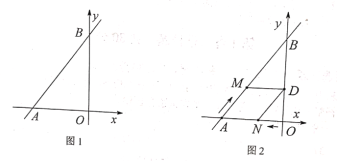
(1)直接写出直线![]() 的解析式;
的解析式;
(2)如图1,过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)如图2,点![]() 从
从![]() 出发以每秒1个单位的速度沿
出发以每秒1个单位的速度沿![]() 方向运动,同时点
方向运动,同时点![]() 从
从![]() 出发以每秒0.6个单位的速度沿
出发以每秒0.6个单位的速度沿![]() 方向运动,运动时间为
方向运动,运动时间为![]() 秒(
秒(![]() ),过点
),过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,是否存在满足条件的
,是否存在满足条件的![]() ,使四边形
,使四边形![]() 为菱形,判断并说明理由.
为菱形,判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
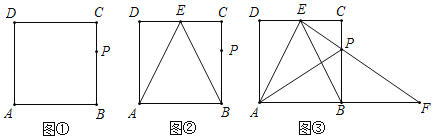
【题目】如图,在矩形ABCD中,AB═2,AD=![]() ,P是BC边上的一点,且BP=2CP.
,P是BC边上的一点,且BP=2CP.
(1)用尺规在图①中作出CD边上的中点E,连接AE、BE(保留作图痕迹,不写作法);
(2)如图②,在(1)的条体下,判断EB是否平分∠AEC,并说明理由;
(3)如图③,在(2)的条件下,连接EP并廷长交AB的廷长线于点F,连接AP,不添加辅助线,△PFB能否由都经过P点的两次变换与△PAE组成一个等腰三角形?如果能,说明理由,并写出两种方法(指出对称轴、旋转中心、旋转方向和平移距离)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1 的正方体搭成的立体图形,第(1)个图形由1个正方体搭成,第(2)个图形由4个正方体搭成,第(3)个图形由10个正方体搭成,以此类推,搭成第(6)个图形所需要的正方体个数是( )
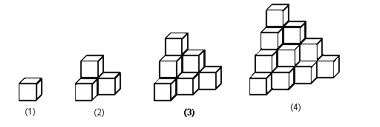
A.84个B.56个C.37个D.36个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
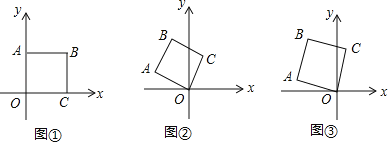
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点.
(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com