
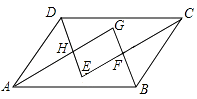
【题目】如图,在ABCD中,各内角的平分线分别相交于点E,F,G,H.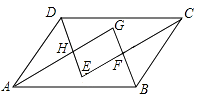
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
【答案】
(1)证明:∵GA平分∠BAD,EC平分∠BCD,
∴∠BAG= ![]() ∠BAD,∠DCE=
∠BAD,∠DCE= ![]() ∠DCB,
∠DCB,
∵ABCD中,∠BAD=∠DCB,AB=CD,
∴∠BAG=∠DCE,
同理可得,∠ABG=∠CDE,
∵在△ABG和△CDE中,
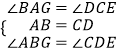 ,
,
∴△ABG≌△CDE(ASA);
(2)解:四边形EFGH是矩形.
证明:∵GA平分∠BAD,GB平分∠ABC,
∴∠GAB= ![]() ∠BAD,∠GBA=
∠BAD,∠GBA= ![]() ∠ABC,
∠ABC,
∵ABCD中,∠DAB+∠ABC=180°,
∴∠GAB+∠GBA= ![]() (∠DAB+∠ABC)=90°,
(∠DAB+∠ABC)=90°,
即∠AGB=90°,
同理可得,∠DEC=90°,∠AHD=90°=∠EHG,
∴四边形EFGH是矩形;
(3)解:依题意得,∠BAG= ![]() ∠BAD=30°,
∠BAD=30°,
∵AB=6,
∴BG= ![]() AB=3,AG=3
AB=3,AG=3 ![]() =CE,
=CE,
∵BC=4,∠BCF= ![]() ∠BCD=30°,
∠BCD=30°,
∴BF= ![]() BC=2,CF=2
BC=2,CF=2 ![]() ,
,
∴EF=3 ![]() ﹣2
﹣2 ![]() =
= ![]() ,GF=3﹣2=1,
,GF=3﹣2=1,
∴矩形EFGH的面积=EF×GF= ![]() .
.
【解析】(1)利用平行四边形的对角、对边相等性质,运用角边角证出全等;(2)平行四边形的一组邻角是同旁内角,两角平分线互相垂直,可得四边形EFGH是矩形;(3)要求矩形EFGH的面积,可求EF、FG,须求BF、CF,在Rt△BCF中可求出BF、CF.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是正方形ABCD对角线BD的中点.
(1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.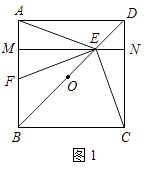
①∠AEM=∠FEM; ②点F是AB的中点;
(2)如图2,若点E是OD上一点,点F是AB上一点,且使 ![]() =
= ![]() =
= ![]() ,请判断△EFC的形状,并说明理由;
,请判断△EFC的形状,并说明理由;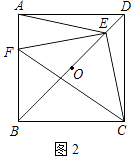
(3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 ![]() =
= ![]() 时,请猜想
时,请猜想 ![]() 的值(请直接写出结论).
的值(请直接写出结论).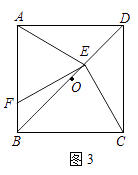
查看答案和解析>>
科目:初中数学 来源: 题型:
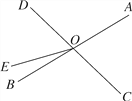
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,若∠DCE=35°,则∠ACB=_____;若∠ACB=140°,则∠DCE=_______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图2,若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且与EF交于点O,那么与∠AOE相等的角有( )
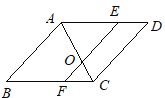
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )

A. 4nB. 4mC. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com