Question

11．在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．
独立探究：
（1）如图1，当点O为AC的中点时，三角板的两直角边分别交AB，BC于E、F两点，猜想线段OE、OF之间的数量关系，并说明理由；
（2）如图2，当点O不是AC的中点时，三角板的两直角边分别交AB，BC于E、F两点，若$\frac{AO}{AC}$=$\frac{1}{4}$，求$\frac{OE}{OF}$的值；
变式拓展：
（3）如图3，三角板的两直角边分别交AB、BC的延长线于E、F两点，若$\frac{AO}{OC}$=$\frac{n}{m}$，直接写出$\frac{OE}{OF}$的值．

Answer 1

分析 （1）OE=OF，如图1，作辅助线，构建全等三角形，证明△EOG≌△FOH即可得出结论；
（2）如图2，同理作辅助线，构建相似三角形，先通过平行相似得：OG=$\frac{1}{4}$BC，OH=$\frac{3}{4}$AB=$\frac{3}{4}$BC，再证明△GOE∽△HOF列比例式可以得结论；
（3）如图3，同理作辅助线，构建相似三角形，先通过平行相似得：OG=$\frac{n}{m+n}$BC，OH=$\frac{m}{m+n}$AB=$\frac{m}{m+n}$BC，再证明△GOE∽△HOF列比例式可以得结论．

解答 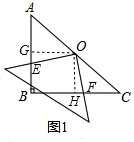解：（1）OE=OF，理由是：
如图1，过O作OG⊥AB于G，OH⊥BC于H，则∠OGE=∠OHF=90°，
∵∠B=90°，
∴OG∥BC，OH∥AB，
∵O是AC的中点，
∴AG=BG，BH=HC，
∴OG=$\frac{1}{2}$BC，OH=$\frac{1}{2}$AB，
∵AB=BC，
∴OG=OH，
∵∠EOF=90°，
∴∠EOH+∠HOF=90°，
∵∠GOH=90°，
∴∠GOE+∠EOH=90°，
∴∠HOF=∠GOE，
∴△EOG≌△FOH，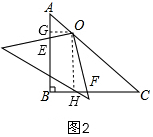
∴OE=OF；
（2）如图2，过O作OG⊥AB于G，OH⊥BC于H，
∵OG∥BC，
∴△AGO∽△ABC，
∴$\frac{OG}{BC}=\frac{AO}{AC}$=$\frac{1}{4}$，
∴OG=$\frac{1}{4}$BC，
同理得：$\frac{OH}{AB}=\frac{OC}{AC}$=$\frac{3}{4}$，
∴OH=$\frac{3}{4}$AB=$\frac{3}{4}$BC，
同理得：∠OGE=∠OHF=90°，∠HOF=∠GOE，
∴△GOE∽△HOF，
∴$\frac{OE}{OF}=\frac{OG}{OH}$，
∴$\frac{OE}{OF}$=$\frac{\frac{1}{4}BC}{\frac{3}{4}BC}$=$\frac{1}{3}$；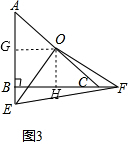
（3）如图3，过O作OG⊥AB于G，OH⊥BC于H，
∵$\frac{AO}{OC}$=$\frac{n}{m}$，
∴$\frac{AO}{AC}$=$\frac{n}{m+n}$，
∵OG∥BC，
∴△AGO∽△ABC，
∴$\frac{OG}{BC}=\frac{AO}{AC}$=$\frac{n}{m+n}$，
∴OG=$\frac{n}{m+n}$BC，
同理得：$\frac{OH}{AB}=\frac{OC}{AC}$=$\frac{m}{m+n}$，
∴OH=$\frac{m}{m+n}$AB=$\frac{m}{m+n}$BC，
同理得：△GOE∽△HOF，
∴$\frac{OE}{OF}=\frac{OG}{OH}$，
∴$\frac{OE}{OF}$=$\frac{\frac{n}{m+n}BC}{\frac{m}{m+n}BC}$=$\frac{n}{m}$．

点评 本题是相似三角形的综合题，难度适中，考查了相似三角形的性质和判定、三角形的中位线定理、等腰直角三角形的性质，做好本题的关键是熟练掌握相似三角形的判定，常用平行或两角对应相等证明两三角形相似；本题的三个问题证明方法类似，都是通过相同的辅助线作法构建全等三角形可相似三角形得出结论．