
在一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.
1.第一小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图1);再沿GC折叠,使点B落在EF上的点B'处(如图2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.

2.第二小组的同学,在一个矩形纸片上按照图3的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图4.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15,请你帮助该小组求出a可能的最大整数值.

3.探究活动结束后,老师给大家留下了一道探究题:如图5,已知AA'=BB'=CC'=2,∠AOB'=∠BOC'=∠COA'=60°,请利用图形变换探究S△AOB'+S△BOC'+S△COA'与的大小关系.

1.连接BB',由题意得EF垂直平分BC,故BB'=B'C,由翻折可得,
B'C=BC,∴△BB'C为等边三角形.∴∠B'CB=60°,
(或由三角函数FC:B'C=1:2求出∠B'CB=60°也可以.)
∴∠B'CG=30°,∴∠B'GC=60°………………………………………3分
2.分别取CE、EG、GI的中点P、Q、R,连接DP、FQ、HR、AD、AF、AH,∵△ABC中,BA=BC,根据平移变换的性质,△CDE、△EFG和△GHI都是等腰三角形,∴DP⊥CE,FQ⊥EG,HR⊥GI.
在Rt△AHR中,AH=AI=4a,AH2=HR2+AR2,HR2=a2,
则DP2=FQ2=HR2=a2,
AD2=AP2+DP2=6a2,AF2=AQ2+FQ2=10a2,
新三角形三边长为4a、a、a.
∵AH2=AD2+AF2 ∴新三角形为直角三角形.
其面积为aa=a2.∵a2<15 ∴a2<15
(或通过转换得新三角形三边就是AD、DI、AI,即求△GAI的面积或利用△HAI与△HGI相似,求△HAI的面积也可以)
∴a的最大整数值为3.………………………………………………7分
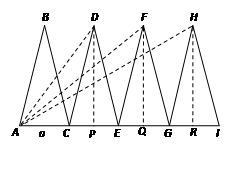
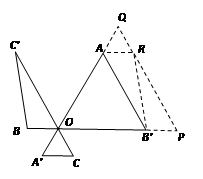
3.将△BOC'沿BB'方向平移2个单位,所移成的三角形记为△B'PR,
将△COA'沿A'A方向平移2个单位,所移成的三角形记为△AQR.
由于OQ=OA+AQ=OA+OA'=AA'=2,OP=OB'+B'P=OB'+OB=BB'=2.又∠QOP=60°,则PQ=OQ=OP=2,
又因为QR+PR=OC+OC',故O、R、P三点共线.因为S△QOP=,
所以S△AOB'+S△BOC'+S△COA'=S△AOB'+S△B'PR+S△PQA< …………10分
解析:所谓的难题就是一些知识点的综合,此题包括了图形的平移、等腰三角形的性质、三角形面积等知识,有一定的难度。


科目:初中数学 来源: 题型:
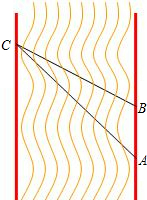 在一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
在一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈| 3 |
| 5 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
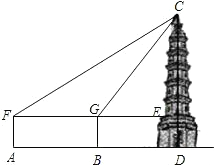 时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.| 3 |
| 5 |
| 3 |
| 4 |
| 9 |
| 25 |
| 3 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.
在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次数学活动课上,王老师给学生发了一块长40cm,宽30cm的长方形纸片(如图),要求折成一个高为5cm的无盖的且容积最大的长方体盒子.
在一次数学活动课上,王老师给学生发了一块长40cm,宽30cm的长方形纸片(如图),要求折成一个高为5cm的无盖的且容积最大的长方体盒子.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com