
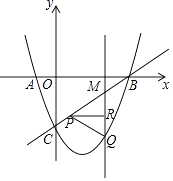
【题目】如图,抛物线y=ax2﹣(a+1)x﹣3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
(1)求抛物线的表达式;
(2)当m=2时,△PQR为等腰直角三角形,求点P的坐标;
(3)①求PR+QR的最大值;②求△PQR面积的最大值.
【答案】
(1)
解:在y=ax2﹣(a+1)x﹣3中,令x=0可得y=﹣3,
∴C(0,﹣3),即OC=3,
∵∠BCO=45°,
∴OB=OC=3,
∴B(3,0),
把B点坐标代入抛物线解析式可得9a﹣3(a+1)﹣3=0,求得a=1,
∴抛物线的表达式为y=x2﹣2x﹣3
(2)
解:当m=2时,则M(2,0),
把x=2代入抛物线解析式可得y=﹣3,
∴Q(2,﹣3),
∵B(3,0),C(0,﹣3),
∴直线BC表达式为y=x﹣3,
∴可设P(p,p﹣3),则PR=2﹣p,QR=p﹣3﹣(﹣3)=p,
∵PR=QR,
∴2﹣p=p,解得p=1,
∴P(1,﹣2)
(3)
解:①由(2)可知M(m,m﹣3),Q(m,m2﹣2m﹣3),
∵PR⊥MQ,
∴∠MPR=45°,
∴MR=PR,
∴PR+QR=PR+MR=QM=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣1<0,
∴当m= ![]() 时,PR+QR取最大值
时,PR+QR取最大值 ![]() ;
;
②∵PR+QR的最大值为 ![]() ,
,
∴S△PQR= ![]() PRQR≤
PRQR≤ ![]() PR(
PR( ![]() ﹣PR)=﹣
﹣PR)=﹣ ![]() (PR﹣
(PR﹣ ![]() )2+
)2+ ![]() ,
,
∵ ![]() <0,
<0,
∴当PR= ![]() 时,△PQR的面积取得最大值
时,△PQR的面积取得最大值 ![]() .
.
【解析】(1)可先求得C点坐标,利用∠BCO=45°可求得B点坐标,代入抛物线解析式可求得a,可求得抛物线解析式;(2)可先求得Q的坐标,利用待定系数法可求得直线BC解析式,设出P点坐标,则可表示出PR、QR的长,由等腰三角形的性质可得到关于P点坐标的方程,可求得P点坐标;(3)①由题意可知PR=RM,故PR+QR=MQ,设出可用m表示出Q点坐标,则可表示出MQ的长,利用二次函数的性质可求得其最大值;②用PR表示出△PQR的面积,利用二次函数的性质可求得其最大值.


科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:BE=AD;
(2)求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“足球进校园”的号召,某学校决定在商场购买甲、乙两种品牌的足球.已知乙种品牌足球比甲种品牌足球每只贵10元,该校欲分别花费2000元、1200元购买甲、乙两种足球,这样购得甲种足球的数量是购得乙种足球的数量的2倍.求甲、乙两种足球的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1= ![]() 的图象与一次函数y2=
的图象与一次函数y2= ![]() x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=
x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1= ![]() 的图象上.
的图象上. 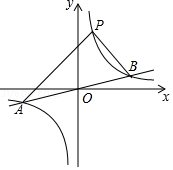
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为-1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )

A. BC=FD,AC=ED B. ∠A=∠DEF,AC=ED
C. AC=ED,AB=EF D. ∠ABC=∠EFD,BC=FD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,AB=AC,点P为边BC上异于B和C的任意一点,过点P作PD⊥AB于D,作PE⊥AC于E,过点C作CF⊥AB于F,求证:PD+PE=CF.

(1)有下面两种证明思路:(一)如图②,连接AP,由△ABP于△ACP面积之和等于△ABC的面积证得PD+PE=CF.(二)如图②,过点P作PG⊥CF,垂足为G,可以证明:PD=GF,PE=CG,则PD+PE=CF.
请你选择其中的一种证明思路完成证明:
(2)探究:如图③,当点P在BC的延长线上时,其它条件不变,探究并证明PD、PE和CF间的数量关系;
(3)猜想:当点P在CB的延长线上时,其它条件不变,猜想PD、PE和CF间的数量关系(不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com