
【题目】如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于________

【答案】60°或120°
【解析】
画出符合的两种情况,过N作NF⊥AD于F,根据HL证出Rt△MFN≌Rt△EDA,即可求出答案.
分为两种情况:①如图1,
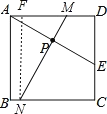
过N作NF⊥AD于F,
则∠NFA=∠MFN=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠B=∠D=90°,
∴四边形AFNB是矩形,
∴NF=AB=AD,
∵∠NFM=∠D=90°,
在Rt△MFN和Rt△EDA中
![]()
∴Rt△MFN≌Rt△EDA(HL),
∴∠AMN=∠AED,
∵∠DAE=30°,∠D=90°,
∴∠AMN=∠AED=180°30°90°=60°;
②如图2,

同法可求Rt△MFN≌Rt△EDA,
所以∠FMN=∠AED=60°,
所以∠AMN=180°60°=120°.
故答案为:60°或120°.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
(1)若AB=2 ![]() ,求BC的长;
,求BC的长;
(2)如图1,当点G在AC上时,求证:BD= ![]() CG;
CG;
(3)如图2,当点G在AC的垂直平分线上时,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有人.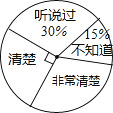
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中考考生最喜欢做哪种类型的英语客观题,2015年志愿者奔赴全市中考各考点对英语客观题的“听力部分、单项选择、完型填空、阅读理解、口语应用”进行了问卷调查,要求每位考生都自主选择其中一个类型,为此随机调查了各考点部分考生的意向.并将调查结果绘制成如图的统计图表(问卷回收率为100%,并均为有效问卷).
被调查考生选择意向统计表
题型 | 所占百分比 |
听力部分 | a |
单项选择 | 35% |
完型填空 | b |
阅读理解 | 10% |
口语应用 | c |
根据统计图表中的信息,解答下列问题:
(1)求本次被调查的考生总人数及a、b、c的值;
(2)将条形统计图补充完整;
(3)全市参加这次中考的考生共有42000人,试估计全市考生中最喜欢做“单项选择”这类客观题的考生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5°
B.15°
C.20°
D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线a∥b,直线c与直线a、b分别相交于C、D两点,直线d与直线a、b分别相交于A、B两点.
(1)如图1,当点P在线段AB上(不与A、B两点重合)运动时,∠1、∠2、∠3之间有怎样的大小关系?请说明理由;
(2)如图2,当点P在线段AB的延长线上运动时,∠1、∠2、∠3之间的大小关系为________;
(3)如图3,当点P在线段BA的延长线上运动时,∠1、∠2、∠3之间的大小关系为________.
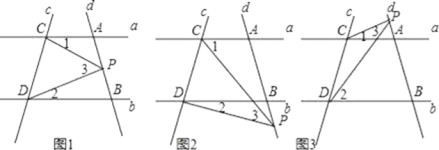
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.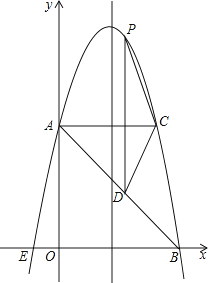
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行与y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点.
(1)若点D在CB上,且DB=1.5cm,AD=6.5cm,求线段CD的长度.
(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB. 
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com