
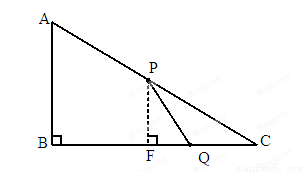
如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒得速度从A点出发,沿AC向C移动,同时,动点Q以1米/秒得速度从C点出发,沿CB向B移动.当其中有一点到达终点时,他们都停止移动,设移动的时间为t秒.

(1)①当t=2.5秒时,求△CPQ的面积;
②求△CPQ的面积S(平方米)关于时间t(秒)的函数关系式.
(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,写出t的值.
(3)以P为圆心,PA为半径的圆与以Q为圆心,QC为半径的圆相切时,求出t的值.
(1)①3.75;②S=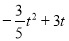 (0<t<5);(2)当
(0<t<5);(2)当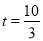 秒;
秒;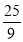 秒;或
秒;或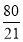 秒时△CPQ为等腰三角形;(3)
秒时△CPQ为等腰三角形;(3)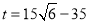 ;
;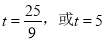
【解析】
试题分析:在Rt△ABC中,AB=6米,BC=8米,所以AC=10米.
由题意得:AP=2t,CQ=10-2t.
(1)①过点P作PD⊥BC于D.
∵t=2.5,AP=2×2.5=5,QC=2.5,
∴PD=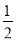 AB=3.
AB=3.
∴S=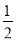 ×QC×PD=3.75.、
×QC×PD=3.75.、

②过点Q作QE⊥PC于点E.
易知Rt△QEC∽Rt△ABC,∴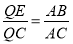 ,QE=
,QE=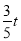 .
.
∴S=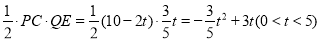 .
.
(2)当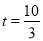 秒(此时PC=QC),
秒(此时PC=QC),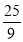 秒(此时PQ=QC),或
秒(此时PQ=QC),或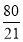 秒(此时PQ=PC)△CPQ为等腰三角形;
秒(此时PQ=PC)△CPQ为等腰三角形;
(3)过点P作PF⊥BC于点F,则有△PCF∽△ACB.
∴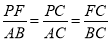 ,即
,即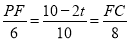 .
.
∴PF=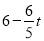 ,FC=
,FC=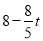 .
.
则在Rt△PFQ中,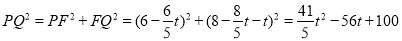 .
.
当⊙P与⊙Q外切时,有PQ=PA+QC=3t,此时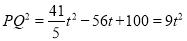 .
.
整理得: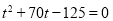 ,解得
,解得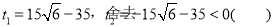 .
.
故⊙P与⊙Q外切时,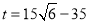 ;
;
当⊙P与⊙Q内切时,有PQ=PA-QC=t,此时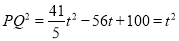 .
.
整理得: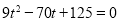 ,解得
,解得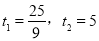 .
.
故⊙P与⊙Q内切时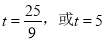 .
.
考点: 三角形的综合运用


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年安徽省淮北市五校七年级上学期期中联考数学试卷(解析版) 题型:解答题
观察下列等式:
第1个等式:a1=  =
=  ×(1﹣
×(1﹣ );第2个等式:a2=
);第2个等式:a2=  =
=  ×(
×( ﹣
﹣ );
);
第3个等式:a3=  =
= ×(
×( ﹣
﹣ );第4个等式:a4=
);第4个等式:a4=  =
=  ×(
×( ﹣
﹣ );
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5=——_=_________;
(2)用含有n的代数式表示第n个等式:an=_________=__________(n为正整数);
(3)求a1+a2+a3+a4+…+a100。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省芜湖县六校九年级上学期第一次联考数学试卷(解析版) 题型:解答题
(10分)如图,抛物线 与x轴交与A(1,0),B(- 3,0)两点.
与x轴交与A(1,0),B(- 3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省威海市环翠区九年级五四制上学期期中考试数学试卷(解析版) 题型:填空题
某型号的电动车如下图所示,它的大灯A射出的光线AB, AC 与地面MN 所夹的锐角分别为8°和10°,大灯A离地面的距离为1m,则该车大灯照亮地面的宽度BC是 m.(参考数据 )
)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省威海市环翠区九年级五四制上学期期中考试数学试卷(解析版) 题型:解答题
如图,抛物线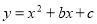 与x轴交于A(-1,0)和B(3,0)两点,交y轴于E.
与x轴交于A(-1,0)和B(3,0)两点,交y轴于E.
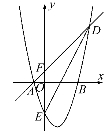
(1)求此抛物线的表达式.
(2)若直线y=x+1与抛物线交于A,D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省章丘市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图所示,河堤横断面迎水坡AB的坡比是1: ,堤高BC=5m,则坡面AB的长度是( )
,堤高BC=5m,则坡面AB的长度是( )

A.10m B.10 m C.15m D.5
m C.15m D.5 m
m
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省章丘市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在△ABC中,EF∥BC, ,
, ,则
,则 ( )
( )

A.9 B.10 C.12 D.13
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省章丘市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分9分) 如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H.

(1)求证: ;
;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求其最大值;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,当0≤t<49时,求S与t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com