
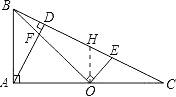
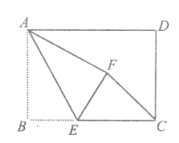
����Ŀ����Rt��ABC�У���BAC=90�㣬AD��BC�ڵ�D����O��AC����һ�㣬����BO����AD�ڵ�F��OE��OB��BC�ڵ�E��
��1����ͼ1����OΪ��AC�е㣬![]() ʱ����
ʱ����![]() ��ֵ.С��������ģ���O����OH��AB��BC�ڵ�H����֤��AOF�ס�HOE����������𰸣�����ֱ��д����
��ֵ.С��������ģ���O����OH��AB��BC�ڵ�H����֤��AOF�ס�HOE����������𰸣�����ֱ��д����![]() ��
��
��2����ͼ2����OΪ��AC�е㣬![]() ʱ�������
ʱ�������![]() ��ֵ,��˵�����ɣ�
��ֵ,��˵�����ɣ�
��3����ͼ3����![]() ,
,![]() ʱ����ֱ��д��
ʱ����ֱ��д��![]() ��ֵ��
��ֵ��

���𰸡�(1)2;(2)![]() ;(3)
;(3) ![]() .
.
��������
��1����֤����BAF=��C����ABF=��COE���ɣ���OH��AC����BC��H����֤����OEH�͡�OFA���ƣ�����֤����ABF�ס�HOE���������������εĶ�Ӧ�ߵı���ȣ����ɵó������ֵ��
��2��ͬ��1���ķ����ó�![]() ���������ɵó����ۣ�
���������ɵó����ۣ�
��3��ͬ��1���ķ����ó�![]() ���������ɵó����ۣ�
���������ɵó����ۣ�
��1��֤������AD��BC��
���DAC+��C=90�㣮
�ߡ�BAC=90�㣬
���BAF=��C��
��OE��OB��
���BOA+��COE=90�㣬
�ߡ�BOA+��ABF=90�㣬
���ABF=��COE��
��O��AC���߽�BC��H����OH��AB��
�ߡ�ABF=��COE����BAF=��C��
���AFB=��OEC��
���AFO=��HEO��
����BAF=��C��
���FAO=��EHO��
���OEH�ס�OFA��
��![]()
�֡�OΪAC���е㣬OH��AB��
��OHΪ��ABC����λ�ߣ�
��OH=![]() AB��OA=OC=
AB��OA=OC=![]() AC��
AC��
��![]() ��2��
��2��
��![]() ��
��
��![]() ��
��
��2��ͬ��1�������ã�![]() ��
��
���֡�OΪAC���е㣬OH��AB��
��OHΪ��ABC����λ�ߣ�
��OH=![]() AB��OA=OC=
AB��OA=OC=![]() AC��
AC��
��![]() ��
��
��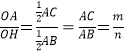 ��
��
��![]() ��
��
��3��ͬ��1�������ã�![]() ��
��
��OH��AB��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C���ҵ�B���C������ֱ�ΪB��3��0����C��0��3������M�������ߵĶ��㣮
��1������κ����Ĺ�ϵʽ��
��2����PΪ�߶�MB��һ�����㣬����P��PD��x���ڵ�D����OD=m����PCD�����ΪS�����ж�S�����ֵ����Сֵ����˵�����ɣ�
��3����MB���Ƿ���ڵ�P��ʹ��PCDΪֱ�������Σ�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪�����߾���![]() ��
��![]() ��
��![]() ���㣮
���㣮
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
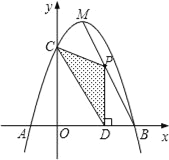
![]() ����MΪ������������������һ���㣬��M�ĺ�����Ϊm��
����MΪ������������������һ���㣬��M�ĺ�����Ϊm��![]() �����ΪS����S����m�ĺ�����ϵʽ�������S�����ֵ��
�����ΪS����S����m�ĺ�����ϵʽ�������S�����ֵ��
![]() ����P���������ϵĶ��㣬��Q��ֱ��
����P���������ϵĶ��㣬��Q��ֱ��![]() �ϵĶ��㣬�ж��м���λ���ܹ�ʹ�õ�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�ϵĶ��㣬�ж��м���λ���ܹ�ʹ�õ�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ����һ�㣬��
����һ�㣬��![]() ��
��![]() �۵���ʹ��
�۵���ʹ��![]() ���ڵ�
���ڵ�![]() ��.����
��.����![]() ����
����![]() Ϊֱ��������ʱ��
Ϊֱ��������ʱ��![]() �ij��ǣ� ��
�ij��ǣ� ��
A.![]() B.
B.![]() C.
C.![]() ��
��![]() D.
D.![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������A��B����![]() ��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20������P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt�루t>0��.
��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20������P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt�루t>0��.
![]()
��1��д�������ϵ�B��ʾ����______����P��ʾ�����ú�t��ʽ�ӱ�ʾ��_______��
��2�����M��AP���е㣬��N��PB���е�.��P��ֱ��AB���˶��Ĺ����У��߶�MN�ij����Ƿ�ᷢ���仯���������仯����˵�����ɣ������仯������߶�MN�ij���.
��3������R�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶�������P��Rͬʱ����������P�˶�������ʱ�����R�ľ���Ϊ2����λ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD���ĸ�����ֱ��ڷ���������![]() ��
��![]() (x��0��0��m��n)��ͼ���ϣ��Խ���BD//y�ᣬ��BD��AC�ڵ�P����֪��B�ĺ�����Ϊ4��
(x��0��0��m��n)��ͼ���ϣ��Խ���BD//y�ᣬ��BD��AC�ڵ�P����֪��B�ĺ�����Ϊ4��
��1����m=4��n=20ʱ��
������P��������Ϊ2����ֱ��AB�ĺ�������ʽ��
������P��BD���е㣬���ж��ı���ABCD����״����˵�����ɣ�
��2���ı���ABCD�ܷ��Ϊ�����Σ����ܣ����ʱm��n֮���������ϵ�������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨:������![]() ��һԪһ�η���
��һԪһ�η���![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ����Ƹ÷���Ϊ���ͽⷽ�̡�������:����
����Ƹ÷���Ϊ���ͽⷽ�̡�������:����![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ����
����![]() �� ��
�� ��![]() Ϊ���ͽⷽ��"������������涨�����������:(1)��֪����
Ϊ���ͽⷽ��"������������涨�����������:(1)��֪����![]() ��һԪһ�η���
��һԪһ�η���![]() �ǡ��ͽⷽ�̡�����
�ǡ��ͽⷽ�̡�����![]() ��ֵΪ________��(2)��֪����
��ֵΪ________��(2)��֪����![]() ��һԪһ�η���
��һԪһ�η���![]() �ǡ��ͽⷽ�̡����������Ľ���
�ǡ��ͽⷽ�̡����������Ľ���![]() ����
����![]() ��ֵΪ_________��
��ֵΪ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪����ABED����C�DZ�DE���е㣬��AB=2AD.
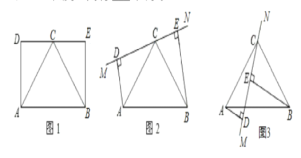
(1)��ͼ1ͨ���۲졢������Եõ��߶�AC���߶�BC��������ϵΪ___��λ�ù�ϵΪ__��
(2)����ͼ1�еġ�ABC�̶�����,�Ƶ�C��תDE���ڵ�ֱ��MN��ͼ2�е�λ��(������AD��BE��ֱ��MN��ͬ��).��̽���߶�AD��BE��DE����֮����ʲô��ϵ?������֤��(��һ���еõ��IJ�����ۿ���ֱ����֤����ʹ��)��
(3)����ͼ2�еġ�ABC�̶�����,�����Ƶ�C��תDE���ڵ�ֱ��MN��ͼ3�е�λ��(�����߶�AD��BE��ֱ��MN�����).��̽���߶�AD��BE��DE����֮����___��ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н�����������Ϊ�˽���о��꼶ѧ����ѧ�ڲμ��ۺ�ʵ������������������˸��й�����ѧ���꼶ѧ����ѧ�ڲμ��ۺ�ʵ�����ʱ�䣬���õõ������ݻ���������������������ͳ��ͼ���������ͼ���ṩ����Ϣ���ش��������⣺
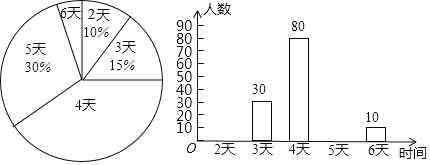
��1���������У���꼶ѧ��������
��2���ֱ�����ʱ��Ϊ2�졢5���ѧ������������ȫ����ͳ��ͼ��
��3��������о��꼶ѧ����Լ50000�ˣ�����������ʱ�䲻����4�������ж����ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com