
【题目】在平面直角坐标系中,已知抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
![]() 求抛物线的解析式;
求抛物线的解析式;
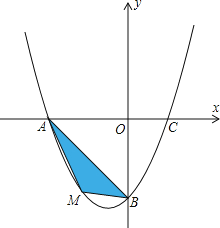
![]() 若点M为第三象限内抛物线上一动点,点M的横坐标为m,
若点M为第三象限内抛物线上一动点,点M的横坐标为m,![]() 的面积为S.求S关于m的函数关系式,并求出S的最大值.
的面积为S.求S关于m的函数关系式,并求出S的最大值.
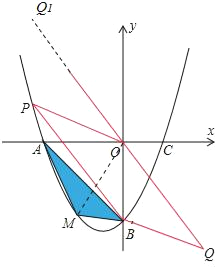
![]() 若点P是抛物线上的动点,点Q是直线
若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
【答案】(1)抛物线的解析式为 y=![]() x+x-4;(2)S= =-(m+2)2+4,4;(3)Q(-4,4)或(-2+2
x+x-4;(2)S= =-(m+2)2+4,4;(3)Q(-4,4)或(-2+2![]() ,2-2
,2-2![]() )或(-2-2
)或(-2-2![]() ,2+2
,2+2![]() )或(4,-4)
)或(4,-4)
【解析】
(1)先假设出函数解析式,利用三点法求解函数解析式.
(2)设出M点的坐标,利用S=S△AOM+S△OBM-S△AOB即可进行解答;
(3)当OB是平行四边形的边时,表示出PQ的长,再根据平行四边形的对边相等列出方程求解即可;当OB是对角线时,由图可知点A与P应该重合.
(1)设此抛物线的函数解析式为:y=ax2+bx+c(a≠0),
将A(﹣4,0),B(0,﹣4),C(2,0)三点代入函数解析式得:
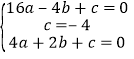 ,解得
,解得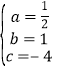 ,
,
所以此函数解析式为:y=![]() x2+x﹣4;
x2+x﹣4;
(2)∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m,![]() m2+m﹣4),
m2+m﹣4),
∴S=S△AOM+S△OBM﹣S△AOB
=![]() ×4×(﹣
×4×(﹣![]() m2﹣m+4)+
m2﹣m+4)+![]() ×4×(﹣m)﹣
×4×(﹣m)﹣![]() ×4×4
×4×4
=﹣m2﹣2m+8﹣2m﹣8
=﹣m2﹣4m,
=﹣(m+2)2+4,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4.
答:m=﹣2时,S有最大值,S=4.
(3)设P(x,![]() x2+x﹣4).
x2+x﹣4).
当OB为边时,根据平行四边形的性质知PQ∥OB,且PQ=OB,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为y=﹣x,
则Q(x,﹣x).
由PQ=OB,得|﹣x﹣(![]() x2+x﹣4)|=4,
x2+x﹣4)|=4,
解得x=0,﹣4,﹣2±2![]() .
.
x=0不合题意,舍去.
如图,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=﹣x得出Q为(4,﹣4).
由此可得Q(4,4)或(﹣2+2![]() ,2﹣2
,2﹣2![]() )或(﹣2﹣2
)或(﹣2﹣2![]() ,2+2
,2+2![]() )或(4,﹣4).
)或(4,﹣4).


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】将自然数按照下表进行排列:
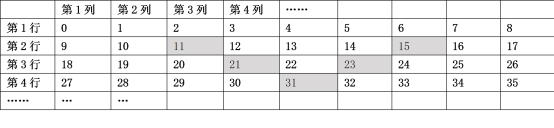
用![]() 表示第
表示第![]() 行第
行第![]() 列数,例如
列数,例如![]() 表示第4行第3列数是29.)
表示第4行第3列数是29.)
(1)已知![]() ,
,![]() _________,
_________,![]() ___________;
___________;
(2)将图中5个阴影方格看成一个整体并在表格内平移,所覆盖的5个自然数之和能否为2021?若能,求出这个整体中左上角最小的数;若不能,请说明理由;
(3)用含![]() 的代数式表示
的代数式表示![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级学生在农场进行社会实践劳动时,采摘了黄瓜和茄子共![]() 千克,了解到采摘的这部分黄瓜和茄子的种植成本共
千克,了解到采摘的这部分黄瓜和茄子的种植成本共![]() 元,还了解到如下信息:黄瓜的种植成本是
元,还了解到如下信息:黄瓜的种植成本是![]() 元/千克,售价是
元/千克,售价是![]() 元/千克;茄子的种植成本是
元/千克;茄子的种植成本是![]() 元/千克,售价是
元/千克,售价是![]() 元/千克.
元/千克.
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子全部卖出可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示
(1)本次共抽查学生____人,并将条形图补充完整;
(2)捐款金额的众数是_____,平均数是_____;
(3)在八年级700名学生中,捐款20元及以上(含20元)的学生估计有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、…、,按一定规律排成如表:
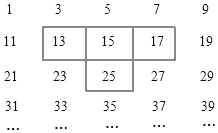
图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数, 若将T字框上下左右移动,则框住的四个数的和不可能得到的数是( )
A.22B.70C.182D.206
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO,交AD于点F,OE⊥OB交BC于点E.
(1)如图1,当O为边AC中点,![]() 时,求
时,求![]() 的值.小明这样想的,过O点作OH∥AB交BC于点H,可证△AOF∽△HOE,于是求出答案,请你直接写出答案
的值.小明这样想的,过O点作OH∥AB交BC于点H,可证△AOF∽△HOE,于是求出答案,请你直接写出答案![]() ;
;
(2)如图2,当O为边AC中点,![]() 时,请求出
时,请求出![]() 的值,并说明理由;
的值,并说明理由;
(3)如图3,当![]() ,
,![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com