
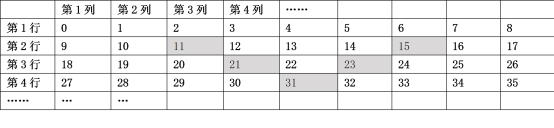
【题目】将自然数按照下表进行排列:
用![]() 表示第
表示第![]() 行第
行第![]() 列数,例如
列数,例如![]() 表示第4行第3列数是29.)
表示第4行第3列数是29.)
(1)已知![]() ,
,![]() _________,
_________,![]() ___________;
___________;
(2)将图中5个阴影方格看成一个整体并在表格内平移,所覆盖的5个自然数之和能否为2021?若能,求出这个整体中左上角最小的数;若不能,请说明理由;
(3)用含![]() 的代数式表示
的代数式表示![]() _________.
_________.
【答案】(1)6,5;(2)不能,理由见解析;(3)![]() .
.
【解析】
(1)观察表中的数据,然后根据数据的变化即可求解;
(2)设其中最小的数为x,则其余4个数可表示为:![]() 、
、![]() 、
、![]() 、
、![]() ,然后利用和为2021建立方程进一步求解,观察其是否符合题意即可;
,然后利用和为2021建立方程进一步求解,观察其是否符合题意即可;
(3)根据表中数据的变化进一步找出代数式即可.
(1)观察表中数据规律加以推算可得:当![]() 时,
时,![]() 6,
6,![]() 5,
5,
故答案为:6,5;
(2)设其中最小的数为x,则其余4个数可表示为:![]() 、
、![]() 、
、![]() 、
、![]() ,
,
则:![]() +
+![]() +
+![]() +
+![]() =2021,
=2021,
即:![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴395是第44行第9列的数,
∵![]() ,其是第45行第4列的数,
,其是第45行第4列的数,
∴二者不在同一行,
∴将图中5个阴影方格看成一个整体并在表格内平移,所覆盖的5个自然数之和不能为2021;
(3)根据题意可得:![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某区举行“中华诵![]() 经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图

根据以上信息,整理分析数据如下:
平均数(分 | 中位数(分 | 众数(分 | |
小学组 | 85 |
| 100 |
中学组 |
| 85 |
|
(1)写出表格中![]() ,
,![]() ,
,![]() 的值:
的值:![]() ,
,![]() ,
,![]() .
.
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴上![]() 两点表示的数分别为
两点表示的数分别为![]() ,则
,则![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)已知数轴上有![]() 两点,点
两点,点![]() 表示的数分别为
表示的数分别为![]() 和40,点
和40,点![]() 以每秒2个单位长度的速度沿数轴向右匀速运动,点
以每秒2个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒3个单位长度的速度沿数轴向左匀速运动.设运动时间为
以每秒3个单位长度的速度沿数轴向左匀速运动.设运动时间为![]() 秒
秒![]() .
.
(1)运动开始前,![]() 两点之间的距离为___________,线段
两点之间的距离为___________,线段![]() 的中点
的中点![]() 所表示的数为__________;
所表示的数为__________;
(2)它们按上述方式运动,![]() 两点经过多少秒会相遇?相遇点所表示的数是多少?
两点经过多少秒会相遇?相遇点所表示的数是多少?
(3)当为多少秒时,线段![]() 的中点
的中点![]() 表示的数为8?
表示的数为8?
(情景扩展)已知数轴上有![]() 两点,点
两点,点![]() 表示的数分别为
表示的数分别为![]() 和40,若在点
和40,若在点![]() 之间有一点
之间有一点![]() ,点
,点![]() 所表示的数为5,点
所表示的数为5,点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左匀速运动,同时,点
以每秒1个单位长度的速度向左匀速运动,同时,点![]() 和点
和点![]() 分别以每秒5个单位长度和2个单位长度的速度向右运动.
分别以每秒5个单位长度和2个单位长度的速度向右运动.
(4)请问:![]() 的值是否随着运动时间
的值是否随着运动时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
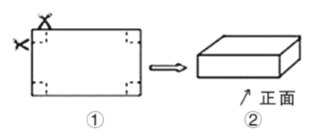
【题目】如图①是一张长为18![]() ,宽为12
,宽为12![]() 的长方形硬纸板,把它的四个角都剪去一个边长为
的长方形硬纸板,把它的四个角都剪去一个边长为![]() 的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积![]()
![]() ;(用含
;(用含![]() 的代数式表示即可,不需化简)
的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当![]() 取什么正整数时,长方体盒子的容积最大?
取什么正整数时,长方体盒子的容积最大?
| 1 | 2 | 3 | 4 | 5 |
| 160 | ________ | 216 | ________ | 80 |
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出![]() 的值;如果不是正方形,请说明理由.
的值;如果不是正方形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
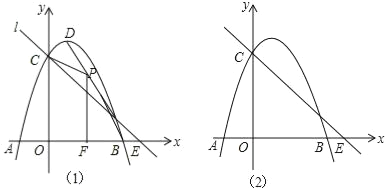
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善生态环境,防止水土流失,某村计划在堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
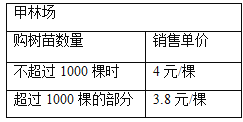
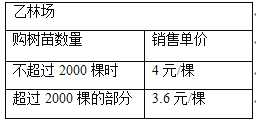
设购买白杨树苗x棵,到两家林场购买所需费用分别为![]() (元)、
(元)、![]() (元). 则:
(元). 则:
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
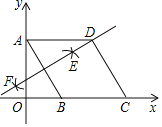
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
A. (2,2)B. (2,![]() )C. (
)C. (![]() ,2)D. (
,2)D. (![]() +1,
+1,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
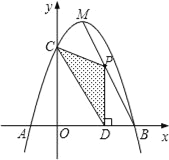
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
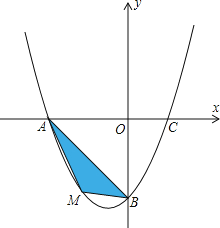
【题目】在平面直角坐标系中,已知抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点M为第三象限内抛物线上一动点,点M的横坐标为m,
若点M为第三象限内抛物线上一动点,点M的横坐标为m,![]() 的面积为S.求S关于m的函数关系式,并求出S的最大值.
的面积为S.求S关于m的函数关系式,并求出S的最大值.
![]() 若点P是抛物线上的动点,点Q是直线
若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com