
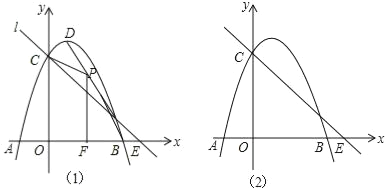
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
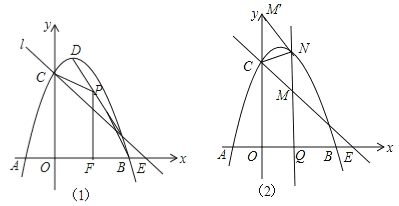
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x+3;(2)
x+3;(2)![]() ;(3)点Q的坐标为(
;(3)点Q的坐标为(![]() ,0)或(4,0).
,0)或(4,0).
【解析】试题(1)先把抛物线解析式配成顶点式即可得到D点坐标,再求出C点坐标,然后利用待定系数法求直线l的解析式;
(2)先根据抛物线与x轴的交点问题求出B(3,0),再利用待定系数法求出直线BD的解析式为y=-2x+6,则P(x,-2x+6),然后根据梯形的面积公式可得S=-x2+![]() x(1≤x≤3),再利用而此函数的性质求S的最大值;
x(1≤x≤3),再利用而此函数的性质求S的最大值;
(3)如图2,设Q(t,0)(t>0),则可表示出M(t,-![]() t+3),N(t,-t2+2t+3),利用两点间的距离公式得到MN=|t2-
t+3),N(t,-t2+2t+3),利用两点间的距离公式得到MN=|t2-![]() t|,CM=
t|,CM=![]() t,然后证明NM=CM得到|t2-
t,然后证明NM=CM得到|t2-![]() t|=
t|=![]() t,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
t,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
试题解析:(1)∵y=-x2+2x+3=-(x-1)2+4,
∴D(1,4),
当x=0时,y=-x2+2x+3=3,则C(0,3),
设直线l的解析式为y=kx+b,
把C(0,3),E(4,0)分别代入得![]() ,解得
,解得 ,
,
∴直线l的解析式为y=-![]() x+3;
x+3;
(2)如图(1),当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,则B(3,0),
设直线BD的解析式为y=mx+n,
把B(3,0),D(1,4)分别代入得![]() ,解得
,解得![]() ,
,
∴直线BD的解析式为y=-2x+6,
则P(x,-2x+6),
∴S=![]()
![]() (-2x+6+3)
(-2x+6+3)![]() x=-x2+
x=-x2+![]() x(1≤x≤3),
x(1≤x≤3),
∵S=-(x-![]() )2+
)2+![]() ,
,
∴当x=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ;
;
(3)存在.
如图2,设Q(t,0)(t>0),则M(t,-![]() t+3),N(t,-t2+2t+3),
t+3),N(t,-t2+2t+3),
∴MN=|-t2+2t+3-(-![]() t+3)|=|t2-
t+3)|=|t2-![]() t|,
t|,
CM=![]() =
=![]() t,
t,
∵△CMN沿CN翻转,M的对应点为M′,M′落在y轴上,
而QN∥y轴,
∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,
∴∠M′CN=∠CNM,
∴∠M′CN=∠CNM′,
∴CM′=NM′,
∴NM=CM,
∴|t2-![]() t|=
t|=![]() t,
t,
当t2-![]() t=
t=![]() t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
当t2-![]() t=-
t=-![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,此时Q点坐标为(
,此时Q点坐标为(![]() ,0),
,0),
综上所述,点Q的坐标为(![]() ,0)或(4,0).
,0)或(4,0).


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
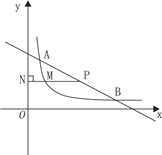
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A,B两点,A点的横坐标为2.
交于A,B两点,A点的横坐标为2.
(1)求点B的坐标;
(2)P为线段AB上一点(不包括端点),P点的纵坐标为a,作PN⊥y轴,垂足为N,交双曲线于点M,求![]() 的最大值;
的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点
上的一个动点![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

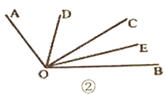
(1)若点![]() 恰好是
恰好是![]() 的中点,则
的中点,则![]() _______
_______![]() ;若
;若![]() ,则
,则![]() _________
_________![]() ;
;
(2)随着点![]() 位置的改版,
位置的改版,![]() 的长是否会改变?如果改变,请说明原因;如果不变,请求出的长;
的长是否会改变?如果改变,请说明原因;如果不变,请求出的长;
(3)知识迁移:如图②,已知![]() ,过角的内部任意一点
,过角的内部任意一点![]() 画射线
画射线![]() ,若
,若![]() 分别平分
分别平分![]() 和
和![]() ,试说明
,试说明![]() 的度数与射线
的度数与射线![]() 的位置无关.
的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
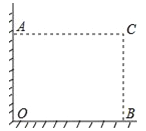
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有五十鹿进舍,小舍容四鹿,大舍容六鹿,需舍几何?(改编自《缉古算经》)”大意为:今有50只鹿进圈舍,小圈舍可以容纳4头鹿,大圈舍可以容纳6头鹿,求所需圈舍的间数.求得的结果有( )
A.3种B.4种C.5种D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将自然数按照下表进行排列:
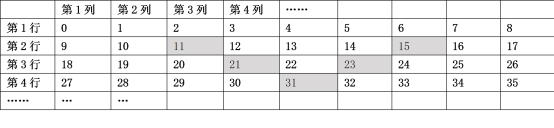
用![]() 表示第
表示第![]() 行第
行第![]() 列数,例如
列数,例如![]() 表示第4行第3列数是29.)
表示第4行第3列数是29.)
(1)已知![]() ,
,![]() _________,
_________,![]() ___________;
___________;
(2)将图中5个阴影方格看成一个整体并在表格内平移,所覆盖的5个自然数之和能否为2021?若能,求出这个整体中左上角最小的数;若不能,请说明理由;
(3)用含![]() 的代数式表示
的代数式表示![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为![]() .若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
.若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
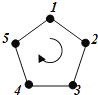
如:小宇同学从编号为![]() 的顶点开始,他应走
的顶点开始,他应走![]() 个边长,即从
个边长,即从![]() 为第一次“移位”,这时他到达编号为
为第一次“移位”,这时他到达编号为![]() 的顶点;然后从
的顶点;然后从![]() 为第二次“移位”,....若小宇同学从编号为
为第二次“移位”,....若小宇同学从编号为![]() 的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计算:当用水量不超过![]() 吨时,每吨的收费标准相同,当用水量超过
吨时,每吨的收费标准相同,当用水量超过![]() 吨时,超出
吨时,超出![]() 吨的部分每吨的收费标准也相同,下表是小明家
吨的部分每吨的收费标准也相同,下表是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
用水量(吨) |
|
|
|
|
费用(元) |
|
|
|
|
请根据表格中提供的信息,回答以下问题:
(1)若小明家![]() 月份用水量为
月份用水量为![]() 吨,则应缴水费________元;
吨,则应缴水费________元;
(2)若某户某月用了![]() 吨水(
吨水(![]() ),应付水费________元;
),应付水费________元;
(3)若小明家![]() 月份交纳水费
月份交纳水费![]() 元,则小明家
元,则小明家![]() 月份用水多少吨?
月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示
(1)本次共抽查学生____人,并将条形图补充完整;
(2)捐款金额的众数是_____,平均数是_____;
(3)在八年级700名学生中,捐款20元及以上(含20元)的学生估计有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com