
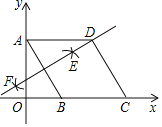
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )
A. (2,2)B. (2,![]() )C. (
)C. (![]() ,2)D. (
,2)D. (![]() +1,
+1,![]()
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】问题提出:用若干个边长为1的小等边三角形拼成![]() 层的大等边三角形,共需要多少个小等边三角形?共有线段多少条?
层的大等边三角形,共需要多少个小等边三角形?共有线段多少条?
图①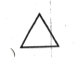 图②
图② 图③
图③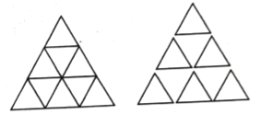
问题探究:
如图①,是一个边长为1的等边三角形,现在用若干个这样的等边三角形再拼成更大的等边三角形.
(1)用图①拼成两层的大等边三角形,如图②,从上往下,第一层有1个,第二层有2个,共用了![]() 个图①的等边三角形,则有长度为1的线段
个图①的等边三角形,则有长度为1的线段![]() 条;还有边长为2的等边三角形1个,则有长度为2的线段
条;还有边长为2的等边三角形1个,则有长度为2的线段![]() 条;所以,共有线段
条;所以,共有线段![]() 条.
条.
(2)用图①拼成三层的大等边三角形,如图③,从上往下,第一层有1个,第二层有2个,第三层有3个,共用了![]() 个图①的等边三角形,则有长度为1的线段
个图①的等边三角形,则有长度为1的线段![]() 条;还有边长为2的等边三角形
条;还有边长为2的等边三角形![]() 个,则有长度为2的线段
个,则有长度为2的线段![]() 条;还有边长为3的等边三角形1个,则有长度为3的线段
条;还有边长为3的等边三角形1个,则有长度为3的线段![]() 条;所以,共有线段
条;所以,共有线段![]() 条.……
条.……
问题解决:
(3)用图①拼成四层的大等边三角形,共需要多少个图①三角形?共有线段多少条?请在方框中画出一个示意图,并写出探究过程;
(4)用图①拼成20层的大等边三角形,共用了 个图①三角形,共有线段 条;
(5)用图①拼成![]() 层的大等边三角形,共用了 个图①三角形,共有线段 条,其中边长为2的等边三角形共有 个.
层的大等边三角形,共用了 个图①三角形,共有线段 条,其中边长为2的等边三角形共有 个.
(6)拓展提升:如果用边长为3的小等边三角形拼成边长为30的大等边三角形,共需要 个小等边三角形,共有线段 条.
查看答案和解析>>
科目:初中数学 来源: 题型:
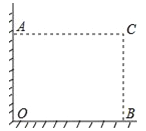
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将自然数按照下表进行排列:
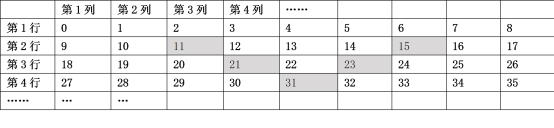
用![]() 表示第
表示第![]() 行第
行第![]() 列数,例如
列数,例如![]() 表示第4行第3列数是29.)
表示第4行第3列数是29.)
(1)已知![]() ,
,![]() _________,
_________,![]() ___________;
___________;
(2)将图中5个阴影方格看成一个整体并在表格内平移,所覆盖的5个自然数之和能否为2021?若能,求出这个整体中左上角最小的数;若不能,请说明理由;
(3)用含![]() 的代数式表示
的代数式表示![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为![]() .若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
.若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
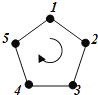
如:小宇同学从编号为![]() 的顶点开始,他应走
的顶点开始,他应走![]() 个边长,即从
个边长,即从![]() 为第一次“移位”,这时他到达编号为
为第一次“移位”,这时他到达编号为![]() 的顶点;然后从
的顶点;然后从![]() 为第二次“移位”,....若小宇同学从编号为
为第二次“移位”,....若小宇同学从编号为![]() 的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运城市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:
A.绿化造林 B.汽车限行 C.拆除燃煤小锅炉 D.使用清洁能源.
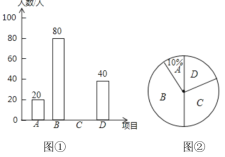
调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整.
(3)求图2中![]() 项目对应的扇形的圆心角的度数.
项目对应的扇形的圆心角的度数.
(4)请你结合自己的实际情况对有效治理雾霾提几点建议.(至少写一条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计算:当用水量不超过![]() 吨时,每吨的收费标准相同,当用水量超过
吨时,每吨的收费标准相同,当用水量超过![]() 吨时,超出
吨时,超出![]() 吨的部分每吨的收费标准也相同,下表是小明家
吨的部分每吨的收费标准也相同,下表是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
用水量(吨) |
|
|
|
|
费用(元) |
|
|
|
|
请根据表格中提供的信息,回答以下问题:
(1)若小明家![]() 月份用水量为
月份用水量为![]() 吨,则应缴水费________元;
吨,则应缴水费________元;
(2)若某户某月用了![]() 吨水(
吨水(![]() ),应付水费________元;
),应付水费________元;
(3)若小明家![]() 月份交纳水费
月份交纳水费![]() 元,则小明家
元,则小明家![]() 月份用水多少吨?
月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级学生在农场进行社会实践劳动时,采摘了黄瓜和茄子共![]() 千克,了解到采摘的这部分黄瓜和茄子的种植成本共
千克,了解到采摘的这部分黄瓜和茄子的种植成本共![]() 元,还了解到如下信息:黄瓜的种植成本是
元,还了解到如下信息:黄瓜的种植成本是![]() 元/千克,售价是
元/千克,售价是![]() 元/千克;茄子的种植成本是
元/千克;茄子的种植成本是![]() 元/千克,售价是
元/千克,售价是![]() 元/千克.
元/千克.
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子全部卖出可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com