
分析 先由平均数的公式计算出这组数据的平均数,再根据方差的公式计算即可.
解答 解:五个监测点的PM2.5的平均值是$\frac{82+91+89+95+73}{5}$=86,
则方差是$\frac{1}{5}$[(82-86)2+(91-86)2+(89-86)2+(95-86)2+(73-86)2]=60.
故答案为:60.
点评 本题考查了方差:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
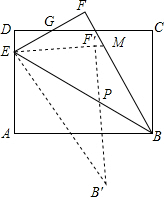 如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.
如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
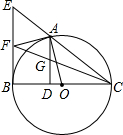 如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G
如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G查看答案和解析>>
科目:初中数学 来源: 题型:解答题
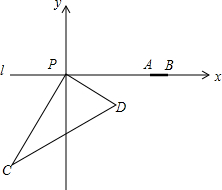 如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10$\sqrt{3}$的D处.
如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10$\sqrt{3}$的D处.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
菱形两对角线长为6和8,则一边上的高等于:( )
A. 5 B. 3 C. 4 D. 4.8
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
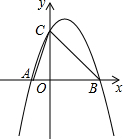 已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则:
已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com