
【题目】某社区计划要对![]() 的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成的绿化面积是乙队每天能完成绿化面积的
的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成的绿化面积是乙队每天能完成绿化面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用
区域的绿化时,甲队比乙队少用![]() 天.
天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工![]() 天,再由乙队施工
天,再由乙队施工![]() 天,刚好完成绿化任务,求
天,刚好完成绿化任务,求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)若甲队每天绿化费用为![]() 万元,乙队每天绿化费用为
万元,乙队每天绿化费用为![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.
天,则如何安排甲、乙两队施工的天数,使施工费用最少?并求出最少费用.
【答案】(1)
甲、乙两工程队每天能完成的面积分别是100m2、50m2;
(2)![]() 与
与![]() 的函数关系式为:y=24﹣2x
的函数关系式为:y=24﹣2x![]() ;
;
(3)甲队的工作10天,则乙队工作4天时, W最少为4.6万元.
【解析】(1)设乙工程队每天能完成绿化的面积是xm2,根据在独立完成面积为300m2区域的绿化时,甲队比乙队少用3天,列方程求解;
(2)用总工作量减去甲队的工作量,然后除以乙队的工作效率即可求解;
(3)设应安排甲队工作a天,乙队的工作天,列不等式组求解.
解:(1)设乙工程队每天能完成绿化的面积是xm2,
根据题意得: ![]() =3,
=3,
解得:x=50,
经检验,x=50是原方程的解,
则甲工程队每天能完成绿化的面积是50×2=100(m2),
答:甲、乙两工程队每天能完成的面积分别是100m2、50m2;
(2)由题意得:100x+50y=1200,
整理得:y=![]() =24﹣2x
=24﹣2x ![]() ;
;
(3)设应甲队的工作a天,则乙队工作b天,( a+b≤14)
根据题意得,100a+50b=1200,
∴b=24﹣2a,a+b≤14,
∴a+24﹣2a≤14,∴a≥10
w=0.4a+0.15b=0.4a+0.15(24﹣2a)=0.1a+3.6,
∴当a=10时,W最少=0.1×10+3.6=4.6万元.
“点睛” 此题是一次函数综合题,主要考查了分式方程及其解法,不等式及其解法,极值的确定,解本题的关键是求出甲乙对每天的工作量.


科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1: ![]() ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留一位小数,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留一位小数, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.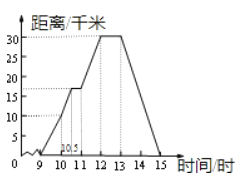
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去括号正确的是( )
A.﹣(2a+b﹣c)=2a+b﹣c
B.﹣2(a+b﹣3c)=﹣2a﹣2b+6c
C.﹣(﹣a﹣b+c)=﹣ab+c
D.﹣(a﹣b﹣c)=﹣a+b﹣c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com